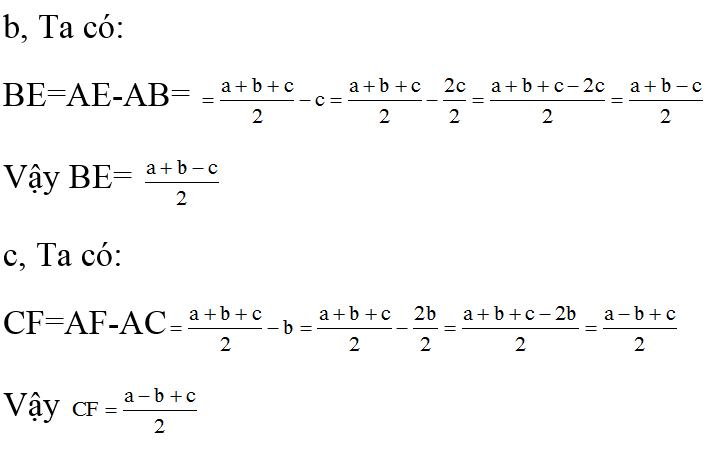Tính chất của hai tiếp tuyến cắt nhau

A. Phương pháp giải

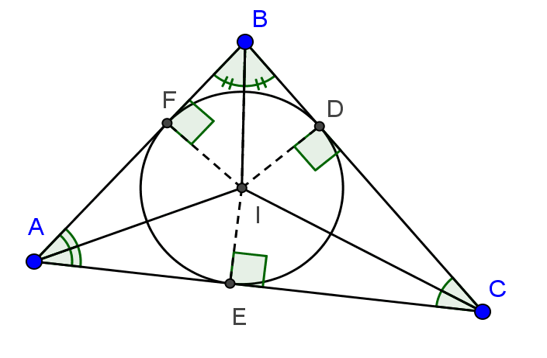
1. Định lí:

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

+ Điểm đó cách đều 2 tiếp điểm.

+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

2. Đường tròn nội tiếp:

Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, cón tam giác gọi là ngoại tiếp đường tròn.

Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác của tam giác đó.

Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.

Tâm của đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B(hoặc C). Với một tam giác , có ba đường tròn bàng tiếp.

B. Bài tập tự luận

Bài 1:

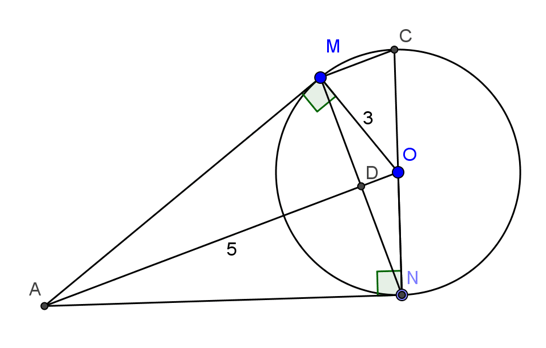
Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm).

a, Chứng minh rằng OA ⊥ MN

b, Vẽ đường kính NOC. Chứng minh rằng MC//AO.

c, Tính độ dài các cạnh của tam giác AMN biết QM=3cm, OA=5cm.

Hướng dẫn giải

a, Ta có:

AM = AN( theo tính chất của 2 tiếp tuyến cắt nhau)

Mà OM = ON( vì cùng bằng R)

Suy ra AO là đường trung trực của MN.

Suy ra OA ⊥ MN

b, Xét tam giác MNC có: NC là đường kính nên suy ra ∠ NMC = 90^o

=> NM ⊥ MC

Mà OA ⊥ MN (chứng minh trên)

MC//OA.

c, Xét tam giác vuông AMO. Theo định lý Py-ta-go ta có:

AM = √(AO² – OM²)(cm) = 4(cm)

Vì AM = AN nên AN = 4cm.

Ta có: OA ⊥ MN (chứng minh trên)

Xét tam giác vuông AMO. Theo hệ thức lượng trong tam giác vuông ta có:

AO.MD = AM.MO

5.MD = 4.3

Suy ra MD = 12/5

Vì MN = 2 MD = 2.12/5 = 24/5(cm)

Vậy AM = AN = 4cm; MN = 24/5 cm.

Bài 2:

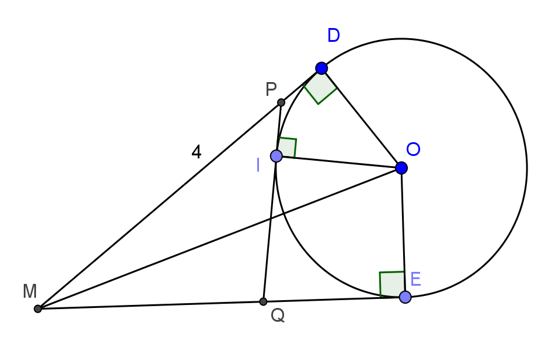
Cho đường tròn(O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD=4cm, tính chu vi tam giác MPQ.

Hướng dẫn giải

Ta có:

+ PD và PI là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại P

Suy ra PD = PI

+ QI và QE là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại Q

Suy ra QI = QE

+ MD và ME là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại M

Suy ra MD = ME

Chu vi tam giác MPQ là: MP + PQ + MQ

= MD- PD + PI + IQ + ME – QE

= MD – PI + PI + QE + MD – QE

= 2MD = 2.4 = 8(cm)

Vậy chu vi tam giác MPQ là 8cm.

Bài 3:

Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB(Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB).Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.

a, Tính số đo góc MON.

b, Chứng minh rằng MN = AM + BN.

c, chứng minh rằng AM.BN = R²(R là bán kính của đường tròn).

Hướng dẫn giải

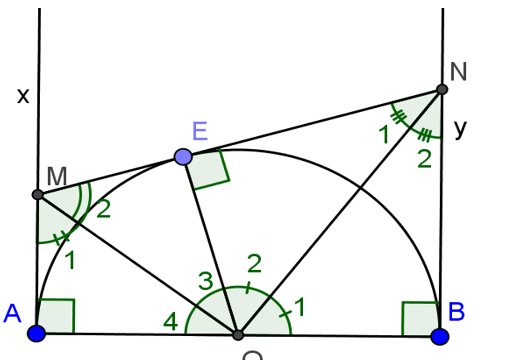
Ta có: NB và NE là 2 tiếp tuyến cắt nhau tại N

=> ∠ O₁ = ∠ O₂; ∠N₁ = ∠ N₂ (theo tính chất 2 tiếp tuyến cắt nhau).

Và OB = OE ; NB = NE (theo tính chất 2 tiếp tuyến cắt nhau).

Ta có: ME và MA là 2 tiếp tuyến cắt nhau tại M

=> O₃ = O₄ và ∠M1 = ∠M2 (theo tính chất 2 tiếp tuyến cắt nhau).

OA=OE; ME=MA ((theo tính chất 2 tiếp tuyến cắt nhau).

Ta có: ∠O₁ + ∠O₂ + ∠O₃ + ∠O₄ = 180^o

Mà ∠O₁ = ∠O₂ và ∠O₃ = ∠O₄ nên suy ra 2∠O₂ + 2∠O₃ = 180^o

=> ∠O₂ + ∠O₃ = 90^p.

b, Ta có: MN = ME + NE = AM + BN(vì ME=MA; NB=NE( chứng minh trên))

c, Ta có: ∠M1 + ∠O₄ = 90^o (vì tam giác MAO vuông tại O)

mà ∠M1 = ∠M2 (chứng minh trên)

=> ∠M2 + ∠O₄ = 90^o

Mặt khác ∠M2 + ∠N₁ = 90^o (vì tam giác MON vuông tại O)

=> ∠O₄ = ∠N₁

Mà ∠N₁ = ∠N₂

Suy ra ∠O₄ = ∠N₂

Xét tam giác MAO và tam giác OBN có:

∠A = ∠B = 90⁰

∠O₄ = ∠N₂ (chứng minh trên)

=> tam giác MAO = tam giác OBN (g-g)

=> MA.BN = AO.OB

=> MA.BN = R² (điều phải chứng minh)

Bài 4:

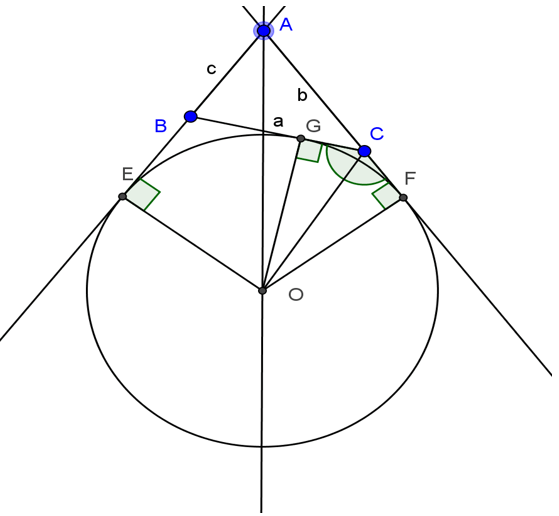
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC=a, AC=b, AB=c. Chứng minh rằng:

a, AE = AF = (a+b+c):2

b, BE = (a+b-c):2

c, CF = (a+c-b):2

Hướng dẫn giải

a, Vì AE và AF là 2 tiếp tuyến cắt nhau tại A nên ta suy ra AE=AF.

Vì BE và BG là 2 tiếp tuyến cắt nhau tại B nên ta suy ra BE=BG.

Vì CG và CF là 2 tiếp tuyến cắt nhau tại C nên ta suy ra CG=CF.

Ta có: AE+AF= AB+BE+AC+CF = AB+BG+AC+GC (vì BE=BG;CG=CF).

= AB + AC + (BG+GC)= AB + AC + BC = a+b+c

Vì AE=AF nên suy ra 2 AF=2 AE=a+b+c

Suy ra AE=AF=(a+b+c):2