Ôn tập chương 2 Hình học 9
A. Bài tập tự luận
Bài 1:
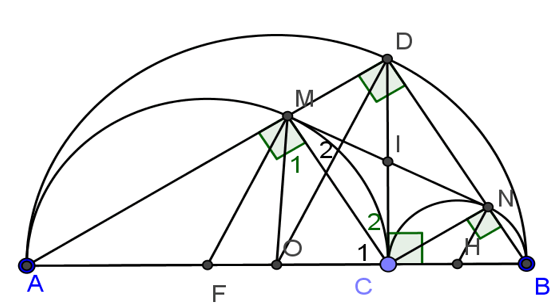
Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA,DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N.
a, Tứ giác DMCN là hình gì? Vì sao?
b, Chứng minh DM.DA=DN.DB
c, Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB.
d, Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất.
Hướng dẫn giải
a, Ta có: Tam giác AMC nội tiếp đường tròn đường kính AC => ∠AMC = 90o
Tam giác CNB nội tiếp đường tròn đường kính CB => ∠CNB = 90o
Tam giác ADB nội tiếp đường tròn đường kính AB => ∠ADB = 900
Suy ra tứ giác DMCN là hình chữ nhật.
b, Xét tam giác vuông DCA có :
DC2 = DM.MA (1) (theo hệ thức lượng trong tam giác vuông)
Xét tam giác vuông DCB có:
DC2 = DN.DB (2) (theo hệ thức lượng trong tam giác vuông)
Từ (1) và (2) ta suy ra DM.MA = DN.NB
c, Vì DMCN là hình chữ nhật nên IM=IC
suy ra tam giác IMC cân tại I
=> ∠M2 = ∠C2
Vì tam giác MFC cân tại F nên ∠M1 = ∠C1
Mà ∠C1 + ∠C2 = 90o => ∠M1 + ∠M2 = 90o
Hay ∠FMN = 90o => FM ⊥ MN
Chứng minh tương tự ∠MNC = 90o => HN ⊥ MN
d, Ta có: DC=MN( vì DMCN là hình chữ nhật)
mà DC ≤ DO => MN ≤ DO
MN = DO khi C ≡ O
Suy ra C là trung điểm của AB.
Bài 2:
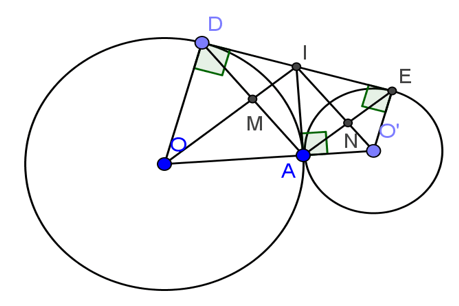
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung DE, D thuộc đường tròn tâm O, E thuộc đường tròn tâm O’. Kẻ tiếp tuyến chung trong tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.
a, Tứ giác AMIN là hình gì? Vì sao?
b, Chứng minh IM.IO=IN.IO’
c, Chứng minh rằng O O’ là tiếp tuyến của đường tròn có đường kính là DE.
d, Tính độ dài DE biết rằng OA=5cm, O’A=3,2 cm.
Hướng dẫn giải
a, ID và IA là 2 tiếp tuyến cắt nhau tại I.
Suy ra ID = IA (1)
Mà OD = OA
Suy ra IO là trung trực của AD
=> IO ⊥ AD => ∠IMA = 90o
+ IE và IA là 2 tiếp tuyến cắt nhau tại I
Suy ra IA=IE (2)
Mà O’A=O’E
Suy ra IO’ là trung trực của AE
=> IO ⊥ AE => ∠INA = 90o
Từ (1) và (2) suy ra IA=ID=IE
Suy ra tam giác DAE vuông tại A
=> ∠DAE = 90o
Tứ giác MINA có 3 góc ∠IMA = 90o ; ∠INA = 90o; ∠DAE = 90o nên tứ giác MINA là hình chữ nhật.
b, Xét tam giác vuông IAO có AN ⊥ IO’ :
IA2 = IM.IO (3) (theo hệ thức lượng trong tam giác).
Xét tam giác vuông IAO’ có :
IA2 = IN.IO’ (4) (theo hệ thức lượng trong tam giác).
Từ (3) và (4) ta suy ra IM.IO = IN.IO’
c, Theo trên ta có tam giác DAE vuông tại A
suy ra 3 điểm D, E, A nội tiếp đường tròn đường kính DE (5)
Do IA là tiếp tuyến chung của 2 đường tròn (O) và (O’)
=> IA ⊥ OO’ (6)
Từ (5) và (6) ta suy ra OO’ là tiếp tuyến của đường tròn đường kính DE.
d, Xét tam giác vuông IOO’
IA2 = OA . OA’
=> IA2 = 5.3,2 =16(cm)
Vậy IA = 4cm.
Bài 3:
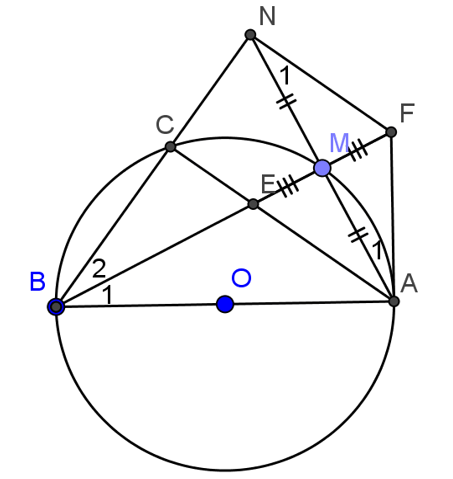
Cho đường tròn (O), đường kính AB, đểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M.BN cắt đường tròn ở C.Gọi E là giao điểm của AC và BM.
a, Chứng minh rằng NE ⊥ AB .
b, Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn(O).
c, Chứng minh rằng FN là tiếp tuyến của đường tròn(B; BA).
Hướng dẫn giải
a, Tam giác AMB nội tiếp đường tròn đường kính AB nên ∠AMB = 90o => AM ⊥ MB
Tam giác ACB nội tiếp đường tròn đường kính AB nên ∠ACB = 90o => AC ⊥ CB
Suy ra E là trực tâm của tam giác NAB, do đó NE ⊥ AB .
b, Tứ giác AFNE có các đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành( tứ giác này còn là hình thoi). Do đó FA//NE.
Do NE ⊥ AB nên FA ⊥ AB .
Suy ra FA là tiếp tuyến của đường tròn (O).
c, Tam giác ABN có đường cao BM cũng là đường trung tuyến nên là tam giác cân. Suy ra BN=BA. Do đó BN là bán kính của đường tròn (B;BA).
Tam giác ABN cân tại B nên ∠BNA = ∠BAN (1)
Tam giác AFN có đường cao FM là đường trung tuyến nên là tam giác cân, suy ra ∠N1 = ∠A1 (2)
Từ (1) và (2) suy ra ∠BNA + ∠N1 = ∠BAN + ∠A1 tức là ∠FNB = ∠FAB
Ta lại có: ∠FAB = 90o (câu b), nên ∠FNB = 90 o . Do đó FN là tiếp tuyến của đường tròn (B).
Bài 4:
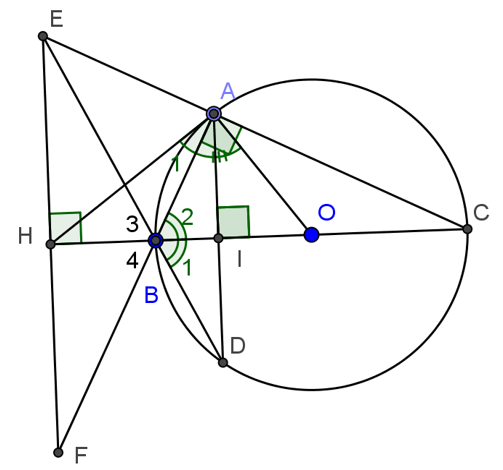
Cho tam giác vuông tại A( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a, Tam giác EBF là tam giác cân.
b, Tam giác HAF là tam giác cân.
c, HA là tiếp tuyến của đường tròn (O)
Hướng dẫn giải
a, Ta có: OB ⊥ AD tại I nên AI=ID.
Suy ra tam giác BAD cân, ∠B1 = ∠B2 , do đó ∠B3 = ∠B4 .
Tam giác EBF có đường cao cũng là đường phân giác nên là tam giác cân.
b, Tam giác BEF cân nên EH = HF.
Tam giác AEF vuông tại A có AH là đường trung tuyến nên AH=HE=HF.
Do đó tam giác HAF cân tại H.
c, Tam giác HAF cân tại H nên ∠A1 = ∠F (1)
Tam giác OAB cân tại O nên ∠OAB = ∠B1 = ∠B4 (2)
Từ (1) và(2) suy ra ∠OAH = ∠A1 + ∠OAB = ∠F + ∠B4 = 90o
Suy ra HA là tiếp tuyến của đường tròn (O).