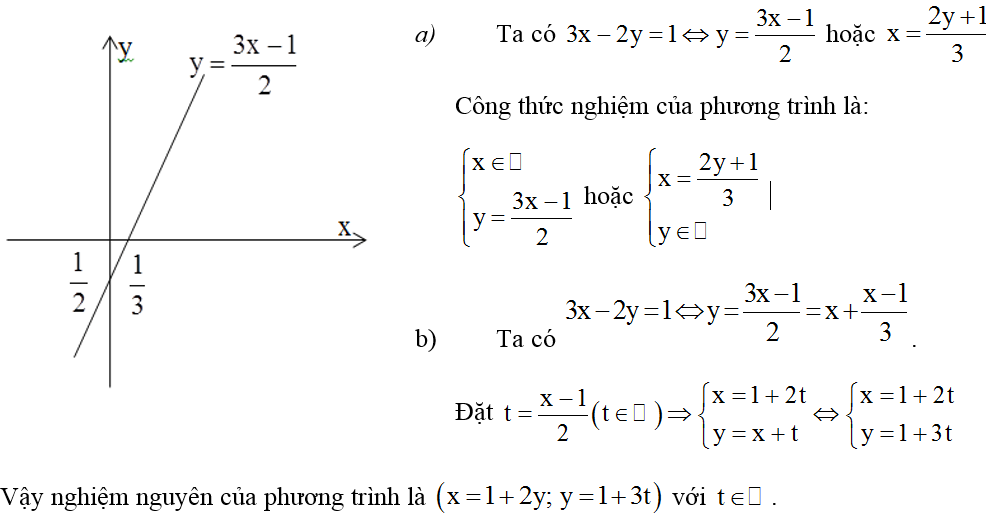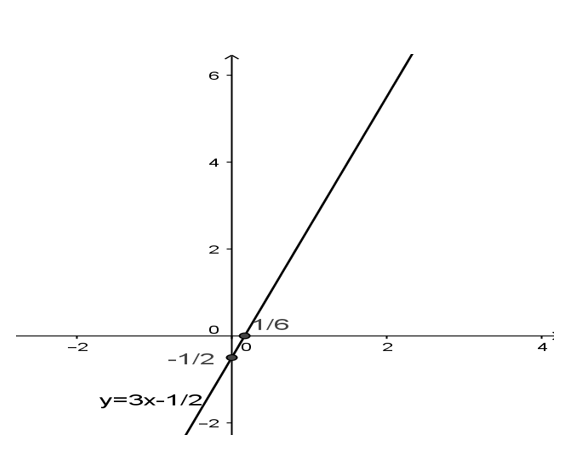Công thức nghiệm của phương trình ax+by=c

A. Phương pháp giải

Tập nghiệm của phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm.

Tập nghiệm của phương trình được biểu diễn bởi đường thẳng (d) ax + by = c.

B. Bài tập tự luận

Bài 1: 

Cho phương trình 3x – 2y = 1

a) Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm trên mặt phẳng tọa độ.

b) Tìm nghiệm của phương trình.

Hướng dẫn giải

Bài 2: 

Xác định phương trình bậc nhất hai ẩn có các nghiệm là (1;-3) và (-2;0). Viết công thức nghiệm tổng quát của phương trình đó.

Hướng dẫn giải

Xét phương trình bậc nhất hai ẩn có dạng tổng quát ax + by = c (a ≠ 0 hoặc b ≠ 0)

+ Thay x = 1; y = -3 và phương trình ta có: a – 3b = c (1)

+ Thay x = -2; y = 0 vào phương trình ta có: -2a = c (2)

Thay (2) vào (1) ta được a – 3b = -2a ⇔ 3a = 3b ⇔ a = b.

Khi đó phương trình có dạng ax + ay = -2a ⇔ x + y = -2 (do a ≠ 0).

Công thức nghiệm tổng quát của phương trình là x ∈ R và y= -x – 2 hoặc x= -y – 2 và y ∈ R

Bài 3: 

Viết công thức nghiệm của các phương trình sau và biểu diễn tập nghiệm trên mặt phẳng tọa độ.

a) 3x – y = 1/2

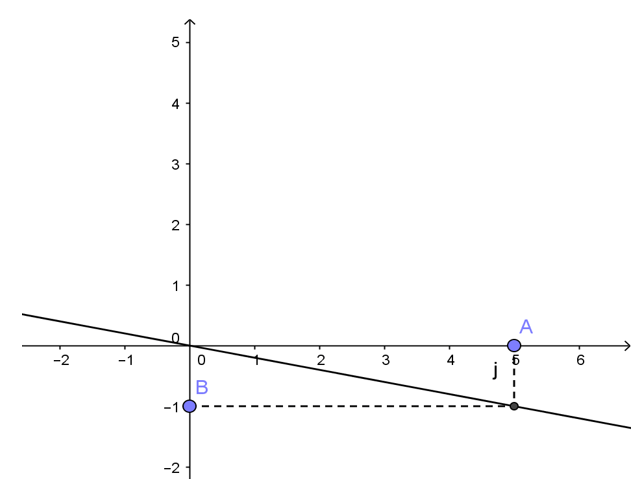
b) x + 5y = 0

Hướng dẫn giải

a) 3x – y = 1/2

Công thức nghiệm tổng quát của phương trình là:

x ∈ R; y = 3x – 1/2

Biểu diễn hình học:

x	0	1/6
y	-1/2	0

b) x + 5y = 0

Công thức nghiệm tổng quát của phương trình là:

x ∈ R; y = -x/5

Biểu diễn hình học

x	0	5
y	0	-1

Bài 4:

Tìm nghiệm nguyên của các phương trình sau:

a) x + 3y = 1

b) 4x – 5y = 24

Hướng dẫn giải