Phương pháp giải phương trình chứa căn bậc hai dạng cơ bản lớp 10 HK 1.

A. Định nghĩa :

y =     Đk : A ≥ 0.

B. Dạng phương trình chứa căn bậc hai cơ bản : 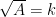  ( k ≥ 0)

 Phương pháp giải :

Bước 1 : Điều kiện : A ≥ 0

Bước 2  :  ⇔ A = k²  ( k ≥ 0)

Ví dụ : giải phương trình chứa căn bậc hai

  (1)

Đk : x+1 ≥  0 ⇔ x  ≥  -1

(1) ⇔ 

⇔ 

 ⇔ x + 1 = 4

⇔x = 3

so đk : x = 3 ≥  -1 (nhận)

vậy : S = {3}

---

C. Dạng phương trình chứa căn bậc hai: 

 Phương pháp giải :

Bước 1 : Điều kiện : Đk : 

Bước 2  :  ⇔ A = B

Ví dụ : phương trình chứa căn bậc hai

   (2)

Điều kiện : Đk : 

⇔ 2x – 2 = 7 – x

⇔ x = 9:3 = 3

so đk : 1 ≤ x = 3 ≤ 7 (nhận)

vậy : S = {3}

D. Dạng phương trình chứa căn bậc hai cơ bản :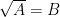 

 Phương pháp giải :

Bước 1 : Điều kiện : A ≥ 0

Bước 2  : bình phương :   => A = B²

Bước 3  : thử nghiệm.

Ví dụ : giải phương trình chứa căn bậc hai

  (3)

Đk : x  –   7  ≥  0 ⇔ x  ≥  7

(3) ⇔ 

=> x  – 7 = (2x – 15)²

⇔ x  – 7 = 4x² – 60x + 225

⇔ 4x² – 61x + 232 = 0

⇔ x = 8 ; x = 29/4

so đk : x = 8 ≥  7  (đúng); và    đúng

 => x = 8 (nhận)

x = 29/4  ≥  7 (đúng) ; và    (sai)

x = 29/4 (loại)

vậy : S = {8}