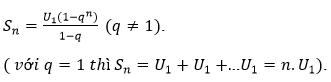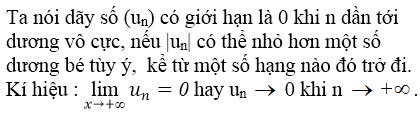Ôn tập cuối năm lớp 11 đại số (phần 2) bài 7,8,9,10,11,12 trang 178 sách giáo khoa lớp 11
Bài 7 (trang 178 SGK Đại số 11): Phát biểu định nghĩa xác suất của biến cố.
Lời giải:
Giả sử A là một biến cố liên quan đến một phép thử với không gian mẫu Ω chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Kí hiệu n(Ω), n(A) theo thứ tự là số các kết quả có thể xảy ra của phép thử và số phần tử của A. Ta gọi là xác suất của biến cố A, kí hiệu P(A) là tỉ số sau:
Bài 8 (trang 178 SGK Đại số 11): Nêu rõ các bước chứng minh bằng quy nạp toán học và cho ví dụ
Lời giải:
Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈N ∗ là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:
Bước 1: Kiểm tra mệnh đề đúng với n =1 .
Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.
Bước 3: Kết luận mệnh đề đúng với n ∈N ∗.
Ví dụ: Chứng minh rằng với mọi n ∈N ∗ ta có:n3+5n chia hết cho 6.
Chứng minh: Đặt P(n) = n3+5n.
Với n =1 => P(1) = 6 ⋮ 6
P(k)=(k3+5k)⋮6.
Ta có: P(k+1)=(k+1)3+5(k+1)=k3+3k2+3k+1+5k+5
=k3+5k+3(k2+k)+6
Mặt khác, theo giả thiết quy nạp ta có: k3+5k)⋮6.
Hơn nữa k2+k=k(k+1):2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).
Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.
Theo nguyên lí quy nạp, ta có P(n) = n3+5n chia hết cho 6 với mọi n ∈N ∗.
Bài 9 (trang 178 SGK Đại số 11): Phát biểu định nghĩa cấp số cộng và công thức tính tổng n số hạng đầu tiên của một số không đổi d.
Lời giải:
Định nghĩa: cấp số cộng là một dãy số ( hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
Ta có: U(n+1) =Un+d , ∀n ∈N ∗
Cho cấp số cộng (Un) công sai d. đặt Sn=U1+U2+..+Un
Khi đó:
Bài 10 (trang 178 SGK Đại số 11): Phát biểu định nghĩa cấp số nhân và công thức tổng n số hạng đầu tiên của một cập số nhân.
Lời giải:
Định nghĩa: Cấp số nhân là một dãy số ( hữu hạn hoặc vô hạn), trong đó từ số hạng thứ hai; mỗi số hạng đều là tích các số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Ta có: U(n+1)=Un.q,∀n ∈N ∗.
Cho cấp số nhân (Un ),công bội q. đặt Sn=U1+U2+..+Un
Khi đó:
Bài 11 (trang 178 SGK Đại số 11): Dãy số Un thỏa mãn điều kiện gì thì được gọi là có giới hạn 0 khi n dần tới dương vô cực?
Lời giải:
Bài 12 (trang 178 SGK Đại số 11): Viết công thức tính tổng của một cấp số nhân lùi vô hạn.
Lời giải: