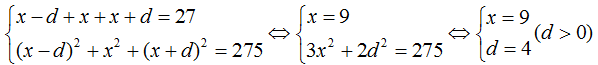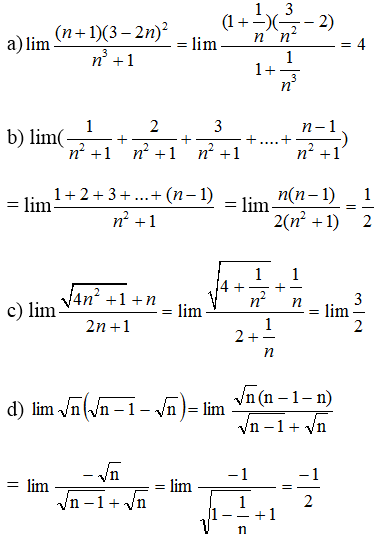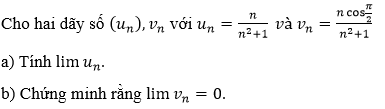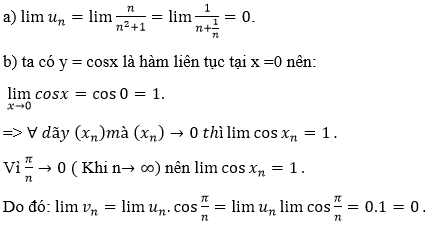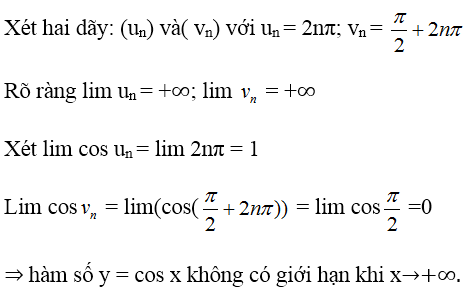Ôn tập cuối năm đại số lớp 11 (phần 5)

Bài 7 (trang 179 SGK Đại số 11): Một tiểu đội có 10 người được xếp ngẫu nhiên thành hàng dọc, trong đó có anh A và anh B. Tính xác xuất sao cho:

a) A và B đứng liền nhau;

b) Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng.

Lời giải:

Mỗi một cách xếp 10 người thành hàng dọc chính là một phần tử của không gian mẫu. Do đó n(Ω)=10!=3628800.

a) A và B đứng liền nhau khi và chỉ khi A và B chia nhau đứng ở hai vị trí: i và i+1 (i=1,2,..9). Ứng với mỗi giá trị i_o xác định i_o=1,2,3 ,…,9) có hai cách sắp xếp A, B vào các vị trí i_o và i_o+1 . Do vậy có tất cả là: 9.2= 18 cách xếp cho A và B đứng liền nhau.Ứng mỗi cách xếp cho A và B đứng cạnh nhau có 8! Cách xếp hàng cho cả 10 người thỏa mãn A, B đứng cạnh nhau. Xác xuất của biến cố này là: P₁=2.9!/10! hay P₁=0,2.

b) Chỉ có đúng 2 cách xếp cho A, và B thỏa mãn yêu cầu bài toán đó là A ở vị trí 1, B ở vị trí 10 hoặc A ở vị trí 10, B ở vị trí 1. Ứng với mỗi cách xếp đó có 8! Cách xếp 10 người thỏa mãn yêu cầu bài toán, từ đây có P₂=2.8!/10!=1/45.

Bài 8 (trang 180 SGK Đại số 11): Tìm một cấp số cộng tăng, biết rằng tổng ba số hạng đầu của nó bằng 27 và tổng các bình phương của chúng bằng 275.

Lời giải:

Gọi công sai của cấp số cộng là d (d > 0) số hạng đầu là u₁ = x – d, u₂ = x, u₃ = x + d.

Theo giả thiết, ta có hệ:

Vậy cấp số cộng đó có u₁ = 5, công sai d = 4.

 

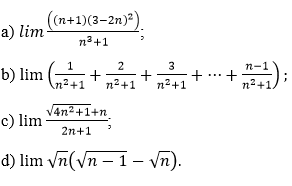
Bài 11 (trang 180 SGK Đại số 11):

Lời giải:

Bài 12 (trang 180 SGK Đại số 11): Chứng minh rằng hàm số y = cosx không có giới hạn khi x → + ∞.

Lời giải:

Bài 12 (trang 180 SGK Đại số 11): Chứng minh rằng hàm số y = cosx không có giới hạn khi x → + ∞.

Lời giải:

Bài 14 (trang 181 SGK Đại số 11): Chứng minh rằng phương trình sau có ít nhất một nghiệm: sin x = x – 1.

Lời giải: