Lý thuyết và bài tập về phương trình đường tròn
Xem thêm phương trình đường tròn lớp 10: các xác định tâm và bán kính, viết phương trình đường tròn
Đường tròn trong lớp 11: đường tròn lượng giác, đường tròn trong phép biến hình dời hình
Đường tròn lớp 12: đường tròn trong mặt cầu, mặt nón, mặt trụ
Đường tròn ngoại tiếp là gì? Đường tròn nội tiếp là gì? định nghĩa, các xác định tâm, tính chất
Một số bài tập liên quan đến đường tròn và phương trình đường tròn

A. Lý thuyết về phương trình đường tròn
1.Lập phương trình đường tròn có tâm và bán kính cho trước
Phương trình đường tròn có tâm I(a; b), bán kính R là :
(x –a)2 + (y – b)2 = R2
2. Nhận xét
Phương trình đường tròn (x – a)2 + (y – b)2 = R2 có thể được viết dưới dạng
x2+ y2 – 2ax – 2by + c = 0
trong đó c = a2 + b2 + R2
Ngược lại, phương trình x2+ y2– 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi và chỉ khi a2 + b2 -c > 0. Khi đó đường tròn (C) có tâm I(a; b) và bán kính R =

3.Phương trình tiếp tuyến của đường tròn

Cho điểm M0(x0 ;y0) nằm trên đường tròn (C) tâm I(a; b).Gọi ∆ là tiếp tuyến với (C) tại M0
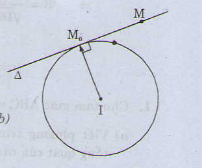
Ta có M0 thuộc ∆ và vectơ (x0– a ; y0 – b) là vectơ pháp tuyến cuả ∆
Do đó ∆ có phương trình là :
(x0 – a )(x – x0 ) + (y0 – b)(y – y0)
Phương trình (1) là phương trình tiếp tuyến của đường tròn
(x –a)2 + (y – b)2 = R2 tại điểm M0 nằm trên đường tròn.
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
Các em có thể học toàn bộ Lý thuyết và bài tập về phương trình đường tròn tại lớp Toán thầy Thế Anh: 0986.683.218
B. Bài tập về phương trình đường tròn
Bài 1 trang 83 sgk hình học 10

1. Tìm tâm và bán kính của các đường tròn sau:
a) x2+ y2– 2x – 2y – 2 = 0
b) 16x2+ 16y2+ 16x – 8y – 11 = 0
c) x2 + y2 – 4x + 6y – 3 = 0.
Hướng dẫn:
a) Ta có : -2a = -2 => a = 1
-2b = -2 => b = 1 => I(1; 1)
R2 = a2 + b2 – c = 12 + 12 – (-2) = 4 => R = 2
b) Tương tự, ta có : I (; R = 1
c) I(2; -3); R = 4
Bài 2 trang 83 sgk hình học 10

2. Lập phương trình đường tròn (C) trong các trường hợp sau:
a) (C) có tâm I(-2; 3) và đi qua M(2; -3);
b) (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng d : x – 2y + 7 = 0
c) (C) có đường kính AB với A(1; 1) và B(7; 5)
Hướng dẫn:
a) Ta tìm bán kính R2 = IM2 => R2 = IM = (2 + 2)2 + (-3 -32) = 52
Phương trình đường tròn (C): (x +2)2 + (y – 3)2 =52
b) Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
d(I; d) = R
Ta có : R = d(I; d)
Phương trình đường tròn cần tìm là:
(x +1)2 + (y – 2)2 = =>( x +1)2 + (y – 2)2
<=> 5x2 + 5y2 +10x – 20y +21 = 0
c) Tâm I là trung điểm của AB, có tọa độ :
x = = 4; y = = 3 => I(4; 3)
AB = 2√13 => R = √13
=> (x -4 )2 + (y – 3)2 =13
Bài 3 trang 83 sgk hình học 10


3. Lập phương trình đường tròn đi qua ba điểm:
a) A(1; 2); B(5; 2); C(1; -3)
b) M(-2; 4); N(5; 5); P(6; -2)

Hướng dẫn:
a) Sử dụng phương trình đường tròn : x2 – y2 – ax – 2by +c = 0
Đường tròn đi qua điểm A(1; 2):
12 + 22 – 2a -4b + c = 0 <=> 2a + 4b – c = 5
Đường tròn đi qua điểm B(5; 2):
52 + 22 – 10a -4b + c = 0 <=> 10a + 4b – c = 29
Đường tròn đi qua điểm C(1; -3):
12 + (-3)2 – 2a + 6b + c = 0 <=> 2a – 6b – c = 10
Để tìm a, b, c ta giải hệ:
Lấy (2) trừ cho (1) ta được phương trình: 8a = 24 => a = 3
Lấy (3) trừ cho (1) ta được phương trình: -10b = 5 => b = – 0,5
Thế a = 3 ; b = -0.5 vào (1) ta tính được c = -1
Ta được phương trình đường tròn đi qua ba điểm A, B, C là :
x2 + y2 – 6x + y – 1 = 0
Chú ý:
Tâm I(x; y) của đường tròn đi qua ba điểm A, B, C là điểm cách đều ba điểm ấy, hay
IA = IB = IC => IA2 = IB2 = IC2
Từ đây suy ra x, y là nghiệm của hệ:
<=> I(3;
Từ đây ta tìm được R và viết được phương trình đường tròn.
b) Ta tính được I(2; 1), R= 5
Phương trình đường tròn đi qua ba điểm M(-2; 4); N(5; 5); P(6; -2) là:
(x – 2)2 + (y – 1)2 = 25 <=> x2 – y2 – 4x – 2y – 20 = 0
Bài 4 trang 83 sgk hình học 10
4. Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm M(2 ; 1)

Hướng dẫn :
Đường tròn tiếp xúc với hai trục tọa độ nên tâm I của nó phải cách đều hai trục tọa độ. Đường tròn này lại đi qua điểm M(2 ; 1), mà điểm M này lại là góc phần tư thứ nhất nên tọa độ của tâm I phải là số dương.
xI= yI > 0
gọi xI= yI = a. Như vậy phương trình đường tròn cần tìm là :
(2 – a)2 + (1 – a)2 = a2
a2 – 6a + 5 = 0 => a = 1 hoặc a = 5
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+ Với a = 1 => (C1) => (x – 1 )2 + (y – 1)2 = 1
x2 + y2 – 2x – 2y + 1 = 0
+ Với a = 1 => (C2) => (x – 5 )2 + (y – 5)2 = 25
x2 + y2 – 10x – 10y + 25 = 0
Bài 5 trang 83 sgk hình học 10
Lập phương trình của đường tròn tiếp xúc với các trục tọa độ và có tâm ở trên đường thẳng d : 4x – 2y – 8 = 0


Hướng dẫn :
Vì đường tròn cần tìm tiếp xúc với hai trục tọa độ nên các tọa độ xI ,yI của tâm I có thể là xI = yI hoặc xI = -yI
Đặt xI = a thì ta có hai trường hợp I(a ; a) hoặc I(-a ; a). Ta có hai khả năng:
Vì I nằm trên đường thẳng 4x – 2y – 8 = 0 nên với I(a ; a) ta có:
4a – 2a – 8 = 0 => a = 4
Đường tròn cần tìm có tâm I(4; 4) và bán kính R = 4 có phương trình:
(x – 4 )2 + (y – 4)2 = 42
x2 + y2 – 8x – 8y + 16 = 0
+ Trường hợp I(-a; a):
-4a – 2a – 8 = 0 => a =
Ta được đường tròn có phương trình:
Bài 6 trang 84 sgk hình học 10
6. Cho đường tròn (C) có phương trình:
x2 + y2 – 4x + 8y – 5 = 0
a) Tìm tọa độ tâm và bán kính của (C)
b) Viết phương trình tiếp tuyến với (C) đi qua điểm A(-1; 0)
c) Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng 3x – 4y + 5 = 0
Hướng dẫn :



a) Tâm I(2 ; -4), R = 5
b) Đường tròn có phương trình: (x – 2 )2 + (y + 4)2 = 25
Thế tọa độ A(-1 ; 0) vào vế trái, ta có :
(-1- 2 )2 + (0 + 4)2 = 32 + 42 = 25
Vậy A(-1 ;0) là điểm thuộc đường tròn.
Áp dụng công thức tiếp tuyến (Xem sgk)
Ta được pt tiếp tuyến với đường tròn tai A là:
(-1 – 2)(x – 2) + (0 + 4)(y + 4) = 25 <=> 3x – 4y + 3 = 0
Chú ý:
1. Theo tính chất tiếp tuyến với đường tròn tại 1 điểm thuộc đường tròn thì vuông góc với bán kính đi qua tiếp điểm, ta có thể giải câu này như sau:
Vectơ = (-3; 4)
Tiếp tuyến đi qua A(-1; 0) và nhận làm một vectơ pháp tuyến có phương trình:
-3(x + 1) + 4(y – 0) = 0 ,<=> 3x – 4y + 3 = 0
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
Kết luận: Lý thuyết và bài tập về phương trình đường tròn sẽ cho các em học sinh tổng quan về đường tròn ở trong chương trình học lớp 10,11,12 và các dạng lý thuyết và bài tập về phương trình đường tròn. Tất cả Lý thuyết và bài tập về phương trình đường tròn sẽ có tại lớp học thêm của thầy Thế Anh