Lý thuyết và bài tập về Hệ trục tọa độ

A. Lý thuyết về Hệ trục tọa độ

1. Trục và độ dài đại số trên trục

a) Trục tọa độ: Trục tọa độ là một đường thẳng trên đó đã xác định một điểm gốc O và một vec tơ đơn vị 

b) Tọa độ của một điểm: Ứng với mỗi điểm M trên trục tọa độ thì có một số thực k sao cho

 = k

Số k được gọi là tọa độ của điểm M đối với trục đã cho.

c) Độ dài đại số: Cho hai điểm A,B trên trục số, tồn tại duy nhất một số a sao cho  = a

a được gọi là độ dài đại số của vectơ  kí hiệu a = 

Chú ý:

– Nếu vectơ cùng hướng với vec tơ đơn vị của trục thì > 0, còn nếu ngược hướng với vec tơ đơn vị thì < 0

– Nếu điểm A có tọa độ trên trục là a và điểm B có tọa độ là b thì

 = b- a

2. Hệ trục tọa độ

a) Định nghĩa: Hệ trục tọa độ (0;   gồm hai trục (0;  và (0;vuôn góc với nhau.

O là gốc tọa độ

(0; ) là trục hoành

(0;) là trục tung

 = = 1

Mặt phẳng được trang bị một hệ tọa độ được gọi là mặt phẳng tọa độ

b) Tọa độ vectơ

=  ⇔ u = (x; y)

hai vectơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau

⇔  x = x’

và y = y’

c) Tọa độ một điểm: Với mỗi điểm M trong mặt phẳng tọa độ thì tọa độ của vec tơ được gọi là tọa độ của điểm M.

⇔  M(x;y)

d) Liên hệ giữa tọa độ của điểm và của vectơ:

cho hai điểm A(x_A; y_A), B(x_B;y_B)

Ta có = (x_A – x_B; y_A – y_B)

Tọa độ của vec tơ thì bằng tọa độ của điểm ngọn trừ đi tọa độ tương ứng của điểm đầu.

3. Tọa độ của tổng, hiệu ,tích của một số với một vectơ

Cho hai vec tơ = (u₁;u₂),       = (v_1; v₂)

Ta có     + = (u₁+ v₁; u₂ + v₂)

–  = (u₁ – v₁; u₂ – v₂)

k.= (ku₁; ku₂).

4. Tọa độ của trung điểm của đoạn thẳng và tọa độ trọng tâm của tam giác

a) Tọa độ trung điểm: Cho hai điểm A(x_A; y_A), B(x_B;y_B) tọa độ của trung điểm I (x_I; y_I) được tính theo công thức:

x_I =  (x_A + x_B)              y_{I = (}y_A + y_B).

b) Tọa độ trọng tâm: Tam giác ABC có 3 đỉnh  A(x_A; y_A), B(x_B;y_B); C(x_C; y_C). Trọng tâm G của tam giác có tọa độ:

x_G = x_A + x_B + x_C)              y_{G =  (}y_A + y_B  + y_C).

[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]

B. Bài tập về Hệ trục tọa độ

Bài 1 trang 26 sgk hình học lớp 10

Bài 1. Trên trục (O, cho các điểm A, B, M có tọa độ lần lượt là -1, 2, 3, -2 .

a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục;

b) Tính độ dài đại số của và . Từ đó suy ra hai vectơ và ngược hướng

 là hai vectơ ngược hướng.

Bài 2 trang 26 sgk hình học lớp 10

Bài 2 Trong mặt phẳng tọa độ các mệnh đề sau đúng hay sai?

a) = (1; 0) là hai vectơ ngược hướng;

b) = (-3; -4) là hai vectơ đối nhau;

c)  = (3; 5) là hai vectơ đối nhau;

d) hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau

Hướng dẫn giải:

a) Đúng                                  b) Đúng

c) Hai vectơ  = (3; 5) không cùng phương nên không thể đối nhau, do vậy câu c) sai

d) Đúng

Bài 3 trang 26 sgk hình học lớp 10

Bài 3. Tìm tọa độ của các vec tơ sau:

 

 

Bài 4 trang 26 sgk hình học lớp 10

Bài 4. Trong mặt phẳng Oxy. Các khẳng định sau đúng hay sai?

a) Tọa độ của điểm A là tọa độ của vec tơ 

b) Điểm A nằm trên trục hoành thì có tung độ bằng 0;

c) Điểm A nằm trên trục tung thì có hoành độ bằng 0;

d) Hoành độ và tung độ của điểm A bằng nhau khi và chỉ khi A nằm trên tia phân giác của góc phần tư thứ nhất.

Hướng dẫn giải:

Các câu a, b, c đúng; d sai

Bài 5 trang 27 sgk hình học lớp 10

Bài 5. Trong các mặt phẳng Oxy cho điểm (x₀; y₀)

a) Tìm tọa độ điểm A đối xứng với M qua trục Ox;

b) Tìm tọa độ điểm B đối xứng với M qua trục Oy;

c) Tìm tọa độ điểm C đối xứng với M qua gốc O.

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.

M₀ (x₀; y₀)=> A(x₀;-y₀) 

b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.

M₀ (x₀; y₀) => B(-x₀;y₀)

c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.

M₀ (x₀; y₀) => C(-x₀;-y₀)

Bài 6 trang 27 sgk hình học lớp 10

Bài 6. Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Tìm tọa độ điểm D.

Hướng dẫn giải:

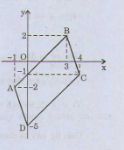
Tứ giác ABCD là hình bình hành nên 

 

 

Bài 7 trang 27 sgk hình học lớp 10

Bài 7. Các điểm A'(-4; 1), B'(2;4), C(2, -2) lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC. Tìm tọa độ đỉnh của tam giác ABC và A’B’C’ trùng nhau.

Hướng dẫn giải:

A’ là trung điểm của cạnh BC nên -4 = x_B+ x_C)

=> x_B+ x_C = -8                        (1)

Tương tự ta có  x_A+ x_C = 4         (2)

                       x_B+ x_{C = 4}          (3)  

=>  x_A+ x_B+ x_{C =0                            (4)}

Kết hợp (4) và (1) ta có:  x_A= 8

             (4) và (2) ta có:  x_B= -4

               (4) và (3) ta có: x_{C = -4}

Tương tự ta tính được: y_A = 1; y_B = -5; y_C = 7.

Vậy A(8;1), B(-4;-5), C(-4; 7).

Gọi G la trọng tâm tam giác ABC thì 

 

Bài 8 trang 27 sgk hình học lớp 10