Lý thuyết và bài tập về Hàm bậc hai y = ax2 + bx + c (a ≠ 0) Toán lớp 10
A. Lý thuyết về Hàm bậc hai y = ax2 + bx + c (a ≠ 0)
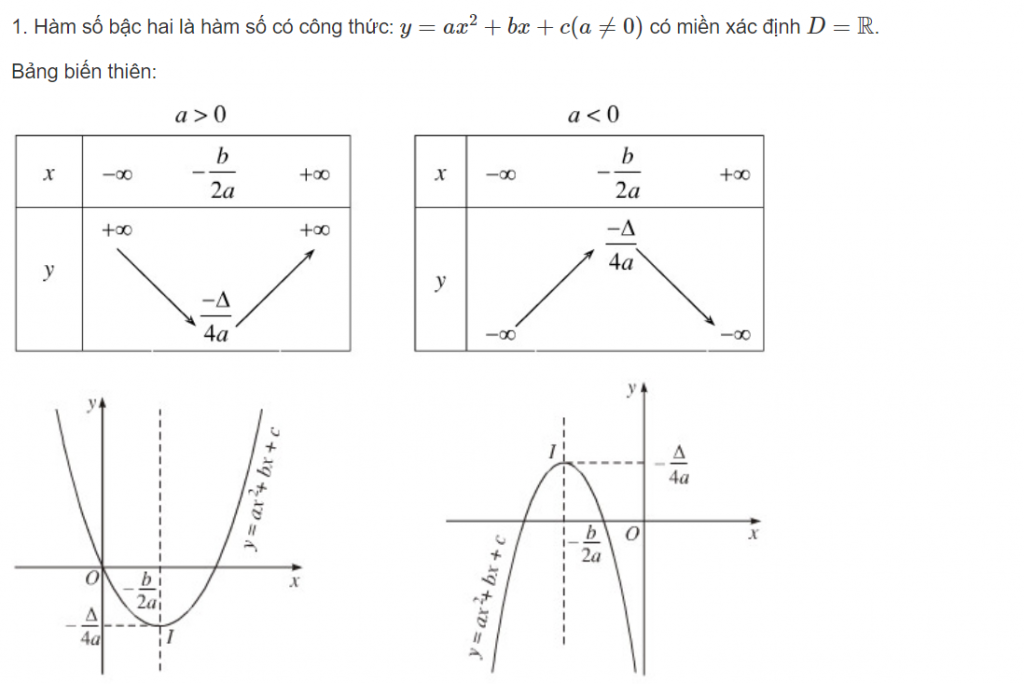

Khảo sát hàm số bậc hai y = ax2 + bx + c (a ≠ 0):
TXĐ : D = R.
Tọa độ đỉnh I (-b/2a; f(-b/2a)). f(-b/2a) = -Δ/4a
Trục đối xứng : x = -b/2a
Tính biến thiên :
- a > 0 hàm số nghịch biến trên (-∞; -b/2a). và đồng biến trên khoảng (-b/2a; +∞)
- a < 0 hàm số đồng biến trên (-∞; -b/2a). và nghịch biến trên khoảng (-b/2a; +∞)
Bảng biến thiên :
a > 0
| x | -∞ | -b/2a | +∞ | ||
| y | +∞ | xuống | f(-b/2a) | lên | +∞ |
a < 0
| x | -∞ | -b/2a | +∞ | ||
| y | -∞ | lên | f(-b/2a) | xuống | -∞ |
Đồ thị :
Đồ thị hàm số ax2 + bx + c là một đường parabol (P) có:
- Đỉnh I (-b/2a; f(-b/2a)).
- Trục đối xứng : x = -b/2a.
- Parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a < 0.
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
B. Bài tập về Hàm bậc hai y = ax2 + bx + c (a ≠ 0)
Bài 1 trang 49 sgk đại số 10
1. Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.
a) y = x2 – 3x + 2; b) y = – 2x2 + 4x – 3;
c) y = x2 – 2x; d) y = – x2 + 4.
Hướng dẫn.


a) y = x2 – 3x + 2. Hệ số: a = 1, b = – 3, c = 2.
- Hoành độ đỉnh x1 =
- Tung độ đỉnh y1 =
Vậy đỉnh parabol là
- Giao điểm của parabol với trục tung là A(0; 2).
- Hoành độ giao điểm của parabol với trục hoành là nghiệm của phương trình:
x2 – 3x + 2 = 0 ⇔ x1 = , x1 =
Vậy các giao điểm của parabol với trục hoành là B(1; 0) và C(2; 0).
b) Đỉnh I(1; 1). Giao điểm với trục tung A(0;- 3).
Phương trình – 2x2 + 4x – 3 = 0 vô nghiệm. Không có giao điểm cuả parabol với trục hoành.
c) Đỉnh I(1;- 1). Các giao điểm với hai trục tọa độ: A(0; 0), B(2; 0).
d) Đỉnh I(0; 4). Các giao điểm với hai trục tọa độ: A(0; 4), B(- 2; 0), C(2; 0).
Bài 2 trang 49 sgk đại số 10
2. Lập bảng biến thiên và vẽ đồ thị của các hàm số.
a) y = 3x2– 4x + 1; b) y = – 3x2 + 2x – 1;
c) y = 4x2– 4x + 1; d) y = – x2 + 4x – 4;
e) y = 2x2+ x + 1; f) y = – x2 + x – 1.
Hướng dẫn
a) Bảng biến thiên:
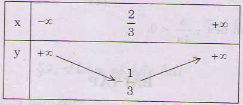
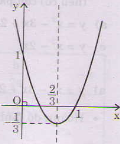
Đồ thị: – Đỉnh:
– Trục đối xứng:
– Giao điểm với trục tung A(0; 1)
– Giao điểm với trục hoành , C(1; 0).
(hình dưới).
b) y = – 3x2 + 2x – 1=
Bảng biến thiên:
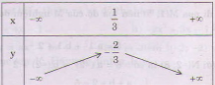
Vẽ đồ thị: – Đỉnh Trục đối xứng:
– Giao điểm với trục tung A(0;- 1).
– Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).
c) y = 4x2 – 4x + 1 =
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) y = – x2 + 4x – 4 = – (x – 2)2
Bảng biến thiên:
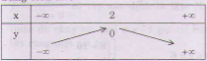
Cách vẽ đồ thị:
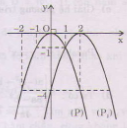
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị (P) của hàm số y = – x2.
+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P1) là đồ thị cần vẽ. (hình dưới).
Bài 3 trang 49 sgk đại số 10
3. Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó:
a) Đi qua hai điểm M(1; 5) và N(- 2; 8);
b) Đi qua hai điểm A(3;- 4) và có trục đối xứng là x=
c) Có đỉnh là I(2;- 2);
d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là
Hướng dẫn.
a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 – x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 – 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 – 3x + 2.
Bài 4 trang 50 sgk đại số 10
4. Xác định a, b, c, biết parabol y = ax2 + bx + c đi qua điểm A(8; 0) và có đỉnh I(6; – 12).
Hướng dẫn.
Ta có hệ phương trình:
Parabol: y = 3x2 – 36x + 96.
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]