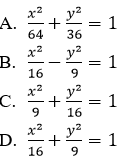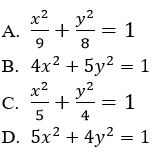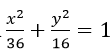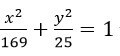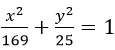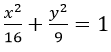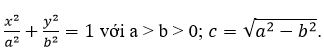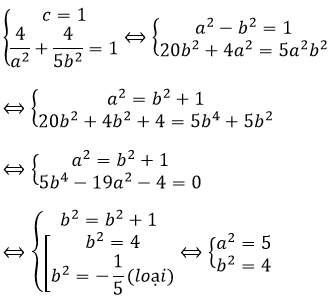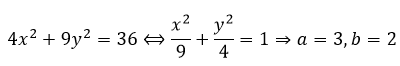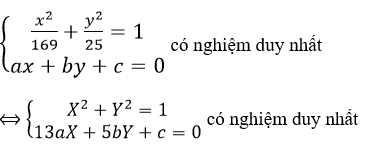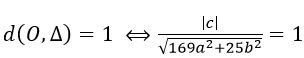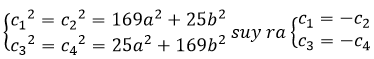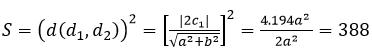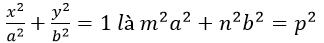Lý thuyết và bài tập về đường Elip – Toán lớp 10
A. Lý thuyết về đường Elip – Toán lớp 10
1. Định nghĩa đường elip
Định nghĩa : Trong mặt phẳng, cho hai điểm cố định F1 và F2
Elip là tập hợp các điểm M sao cho tổng F1M +F2M = 2a không đổi
Các điểm F1 và F2 gọi là tiêu điểm của elip
Khoảng cách F1 .F2 = 2c gọi là tiêu cự của elip
2. Phương trình chính tắc của elip
Cho elip có tiêu điểm F1 và F2 chọn hệ trục tọa độ Oxy sao cho F1(-c ; 0) và F2(c ; 0). Khi đó người ta chứng minh được
M(x ; y) ε elip <=>
 trong đó: b2 = a2 – c2
trong đó: b2 = a2 – c2
Các thông tin của elip (E)
– Hai tiêu điểm: F1(-c;0),F2(c;0).
– Bốn đỉnh A1(-a;0),A2(a;0),B1(0;-b),B2(0;b)
– Độ dài trục lớn: A1A2=2a, độ dài trục nhỏ B1B2=2b
– Tiêu cự: F1F2=2c
– Elip (E) có tâm đối xức là gốc tọa độ, có hai trục đối xức là các trụ tọa độ.
– Bốn đường thẳng x=±a,y=±b tạo thành một hình chữ nhật, gọi là hình chữ nhật cơ sở của elip (E). Hình chữ nhật có chiều dài là 2a và chiều rộng là 2b.
3. Hình dạng của elip
Xét elip (E) có phương trình (1):
a) Nếu điểm M(x; y) thuộc (E) thì các điểm M1(-x ; y) M2(x ;- y) và M3(-x ; -y) cũng thuộc (E).
Vậy (E) có các trục đối xứng là Ox, Oy và có tâm đối xứng là gốc O.
b) Thay y = 0 vào (1) ta có x = ±a suy ra (E) cắt Ox tại hai điểm A1(-a ; 0) A2(a ;0).
Tương tự thay x = 0 vào (1) ta được y = ±b, vậy (E) cắt Oy tại hai điểm B1(0 ; -b) B2(0 ;b).
Các điểm A1, A2, B1, B2 gọi là các đỉnh của elip
Đoạn thẳng A1A2 gọi là trục lớn, đoạn thẳng B1, B2 gọi là trục nhỏ của elip
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
Bài tập trắc nghiệm Hình học 10: Phương trình đường Elip (phần 1)
Câu 1: Phương trình chính tắc của elip có độ dài trục lơn bằng 8, độ dài trục nhỏ bằng 6 là:
Câu 2: Phương trình của elip có 1 tiêu điểm F2(1;0) và đi qua điểm M(2; -2/√5) là:
Câu 3: Cho elip có phương trình 4x2+9y2=36. Khi đó hình chữ nhật cơ sở có diện tích bằng:
A. 6 B. 12 C. 24 D. 36
Câu 4: Cho elip (E) có phương trình
Đường thẳng nào sau đây cắt (E) tại hai điểm đối xứng nhau qua trục Oy?
A. y = 2x B. y = 3 C. x = 3 D. y = 10
Câu 5: Cho elip (E) có phương trình
với hai tiêu điểm là F1,F2. Với điểm M bất kì trên (E) thì chu vi tam giác MF1F1 là:
A. 50 B. 36
C. 34 D. Thay đổi phụ thuộc vào vị trí M
Câu 6: Cho elip (E) có phương trình
và (H) là hình vuông có các cạnh đều tiếp xúc với (E). Khi đó diện tích của (H) là:
A. 194 B. 260 C. 388 D. 288
Hướng dẫn giải và Đáp án
| 1-D | 2-C | 3-C | 4-B | 5-A | 6-C |
Câu 1:
Theo bài ra ta có độ dài trục lớn 2a = 8 => a = 4, độ dài trục nhỏ 2b = 6 => b = 3 nên phương trình chính tắc của elip là
Đáp án là D.
Câu 2:
Phương trình chính tắc của (E) và:
Elip có một tiêu điểm F2(1;0) và đi qua điểm M(2; -2/√5) nên ta có
Đáp án là C.
Câu 3:
Elip có phương trình:
Hình chữ nhật cơ sở có chiều dài là 6 và chiều rộng là 4 nên diện tích là 24.
Đáp án là C.
Câu 4:
Để đường thẳng cắt (E) tại hai điểm đối xứng nhau qua trục Oy thì đường thẳng đó cần song song với trục Ox. Phương án D không thỏa mãn vì không cắt (E).
Đáp án là B.
Câu 5:
Từ phương trình chính tắc của (E) ta có các thông tin về các bán trục và bán tiêu cự a = 13, b = 5, c = 12. Theo định nghĩa của elip ta có MF1+MF2=2a=26,F1F2=2c=24. Chu vi tam giác MF1F2 là 50
Đáp án là A.
Câu 6:
Ta có nhận xét sau: đường thẳng d: ax + by + c = 0 tiếp xúc với (E) khi hệ phương trình
<=> đường thẳng Δ: 13ax + 5by + c = 0 tiếp xúc với đường tròn (C): x2+y2=1
<=>169a2+25b2=c2 (*). Ta gọi hệ thức (*) là điều kiện tiếp xúc của d và (E).
Gọi bốn cạnh của hình vuông là
d1:ax+by+c1=0 ,d2:ax+by+c2=0 ,
d3:ax+by+c3=0,d4:ax+by+c4=0 .
Dùng điều kiện tiếp xúc trên ta có
Do (H) là hình vuông nên d(d1,d2)=d(d3,d4) => |c1|=|c3| => a2 = b2
Ta có c12= c22= c32 = c42 = 194a2 = 194b2.
Diện tích hình vuông (H) là
Đáp án là C.
Chú ý. Trong trường hợp tổng quát ta cũng có điều kiện tiếp xúc của đường thẳng a: mx + ny + p = 0 và elip (E):
Bài 1 trang 88 sgk hình học 10
1. Xác đinh độ dài các trục, tọa độ tiêu điểm , tọa độ các đỉnh và vẽ các elip có phương trình sau:

b) 4x2 + 9y2 = 1
c) 4x2 + 9y2 = 36
Hướng dẫn:

a) Ta có: a2 = 25 => a = 5 độ dài trục lớn 2a = 10
b2 = 9 => b = 3 độ dài trục nhỏ 2a = 6
c2 = a2 – b2 = 25 – 9 = 16 => c = 4
Vậy hai tiêu điểm là : F1(-4 ; 0) và F2(4 ; 0)
Tọa độ các đỉnh A1(-5; 0), A2(5; 0), B1(0; -3), B2(0; 3).
c) Chia 2 vế của phương trình cho 36 ta được :
Từ đây suy ra: 2a = 6. 2b = 4, c = √5
=> F1(-√5 ; 0) và F2(√5 ; 0)
A1(-3; 0), A2(3; 0), B1(0; -2), B2(0; 2).

Bài 2 trang 88 sgk hình học 10
2. Lập phương trình chính tắc của elip, biết:
a) Trục lớn và trục nhỏ lần lươt là 8 và 6
b) Trục lớn bằng 10 và tiêu cự bằng 6
Hướng dẫn:

Phương trình chính tắc của elip có dạng :
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 – 9 = 16
Bài 3:


Bài 4 trang 88 sgk hình học 10
4. Để cắt một bảng hiệu quảng cáo hình elip có các trục lớn là 80cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước 80cm x 40cm, người ta vẽ một hình elip lên tấm ván như hình 3.19. Hỏi phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?

Hướng dẫn:
Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 – 20√3
=> F2A = 20(2 – √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm
Bài 5 trang 88 sgk hình học 10
Cho hai đường tròn C1(F1; R1) và C2(F2; R2). C1 nằm trong C2 và F1 ≠ F2 . Đường tròn (C) thay đổi luôn tiếp xúc ngoài với C1 và tiếp xúc trong với C2.Hãy chứng tỏ rằng tâm M của đường tròn (C) di động trên một elip.
Hướng dẫn:

Gọi R là bán kính của đường tròn (C)
(C) và C1 tiếp xúc ngoài với nhau, cho ta:
MF1 = R1+ R (1)
(C) và C2 tiếp xúc ngoài với nhau, cho ta:
MF2 = R2 – R (2)
Từ (1) VÀ (2) ta được
MF1 + MF2 = R1+ R2= R không đổi
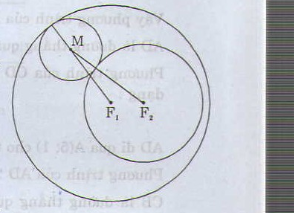
Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1+ R2
Vậy tập hợp điểm M là đường elip, có các tiêu điểm F1 và F2 và có tiêu cự
F1 .F2 = R1+ R2