Ôn tập chương II
Bài 30 trang 69 Sách bài tập Toán 9 Tập 1:
a. Với những giá trị nào của m thì hàm số y = (m + 6)x – 7 đồng biến?
b. Với những giá trị nào của k thì hàm số y = (-k + 9)x – 7 nghịch biến?
Lời giải:
a. Hàm số y = (m + 6)x – 7 đồng biến khi hệ số a > 0
Ta có: m + 6 > 0 ⇔ m > -6
Vậy với m > -6 thì hàm số y = (m + 6)x – 7 đồng biến
b. Hàm số y = (-k + 9)x – 7 nghịch biến khi hệ số a < 0
Ta có: -k + 9 < 0 ⇔ k > 9
Vậy với k > 9 thì hàm số y = (-k + 9)x – 7 nghịch biến.
Bài 31 trang 69 Sách bài tập Toán 9 Tập 1:
Với những giá trị nào của m thì đồ thị của các hàm số:
y = 12x + (5 – m) và y = 3x + (3 + m)
cắt nhau tại một điểm trên trục tung?
Lời giải:
Hai đường thẳng y = 12x + (5 – m) và y = 3x + (3 + m) cắt nhau tại một điểm trên trục tung nghĩa là chúng có cùng tung độ góc.
Suy ra: 5 – m = 3 + m ⇔ 2m = 2 ⇔ m = 1
Vậy với m = 1 thì đồ thị của các hàm số y = 12x + (5 – m) và y = 3x + (3 + m) cắt nhau tại một điểm trên trục tung.
Bài 32 trang 70 Sách bài tập Toán 9 Tập 1:
Tìm giá trị của a để hai đường thẳng: y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau.
Lời giải:
Hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 có tung độ gốc khác nhau do vậy chúng song song với nhau khi và chỉ khi chúng có hệ số a bằng nhau.
Ta có: a – 1 = 3 – a ⇔ 2a = 4 ⇔ a = 2
Vậy với a = 2 thì hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau.
Bài 33 trang 70 Sách bài tập Toán 9 Tập 1:
Với điều kiện nào của k và m thì hai đường thẳng sau trùng nhau?
y = kx + (m – 2)
y = (5 – k)x + (4 – m)
Lời giải:
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi k = 5 – k và m – 2 = 4 – m
Ta có: k = 5 – k ⇔ 2k = 5 ⇔ k = 2,5
m – 2 = 4 – m ⇔ 2m = 6 ⇔ m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau.
Bài 34 trang 70 Sách bài tập Toán 9 Tập 1:
Cho đường thẳng y = (1 – 4m)x + m – 2 (d)
a. Với giá trị nào của m thì đường thẳng (d) đi qua gốc tọa độ?
b. Với giá trị nào của m thì đường thẳng (d) tạo với trục Ox một góc nhọn? Một góc tù?
c. Tìm giá trị của m để đường thẳng (d) cắt trục tung tại một điểm có tung độ bằng 3/2
d. Tìm giá trị của m để đường thẳng (d) cắt trục hoành tại một điểm có hoành độ bằng 1/2
Lời giải:
a. Đồ thị hàm số bậc nhất y = (1 – 4m)x + m – 2 đi qua gốc tọa độ khi 1 – 4m ≠ 0 và m – 2 = 0
Ta có: 1 – 4m ≠ 0 ⇔ m ≠ 1/4
m – 2 = 0 ⇔ m = 2
Vậy với m = 2 thì (d) đi qua gốc tọa độ.
b. Đường thẳng (d) tạo với trục Ox một góc nhọn khi hệ số góc của đường thẳng là số dương.
Ta có: 1 – 4m > 0 ⇔ m < 1/4
Đường thẳng (d) tạo với trục Ox một góc tù khi hệ số góc của đường thẳng là số âm.
Ta có: 1 – 4m < 0 ⇔ m > 1/4
Vậy với m < 1/4 thì đường thẳng (d) tạo với trục Ox một góc nhọn, với m > 1/4 thì đường thẳng (d) tạo với trục Ox một góc tù.
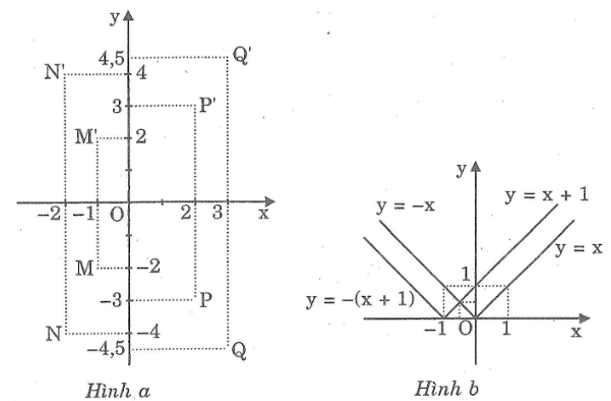
– Vẽ đồ thị hàm số y = -(x + 1)
Cho x = 0 thì y = -1. Ta có: (0; -1)
Cho y = 0 thì x = -1. Ta có: (-1; 0)
Đồ thị hàm số y = -(x + 1) đi qua hai điểm (0; -1) và (-1; 0)
c. Ta có: y = x và y = x + 1 song song với nhau.
y = -x và y = -(x + 1) song song với nhau.
Suy ra chỉ có đồ thị hàm số y = -x và y = x + 1 cắt nhau.
Phương trình hoành độ giao điểm:
-x = x + 1 ⇔ 2x = -1 ⇔ x = – 1/2
Suy ra phương trình |x| = |x + 1| có một nghiệm duy nhất.
Tung độ giao điểm: y = -x ⇒ y = 1/2
Vậy tọa độ giao điểm của đường thẳng y = |x| và y = |x + 1| là:
I(- 1/2 ; 1/2 )