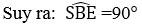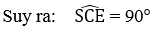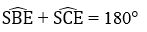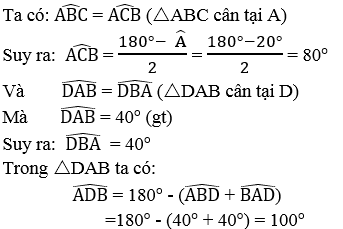Bài 7: Tứ giác nội tiếp
Bài 39 trang 106 Sách bài tập Toán 9 Tập 2:
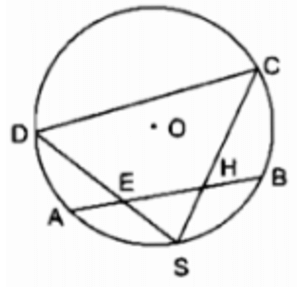
Trên đường tâm O có một cung AB và S là điểm chính giữa của cung đó.Trên dây AB lấy hai điểm E và H.Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D.Chứng minh EHCD là một tứ giác nội tiếp
Lời giải:
Bài 40 trang 106 Sách bài tập Toán 9 Tập 2:
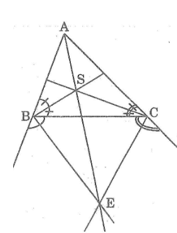
Cho tam giác ABC.Các đường phân giác trong của góc B và góc C cắt nhau tại S,các đường phân giác ngoài của góc B và góc C cắt nhau tại E.Chứng minh BSCE là một tứ giác nội tiếp
Lời giải:
Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)
Xét tứ giác BSCE ta có:
Vậy tứ giác BDCE nội tiếp tròn cung đường tròn
Bài 41 trang 106 Sách bài tập Toán 9 Tập 2:
Cho tam giác ABC có đáy BC và góc A = 20°.Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và góc (DAB) =40°.Gọi E là giao điểm của AB và CD
a.Chứng minh ACBD là một tứ giác nội tiếp
b.Tính góc (AED)
Lời giải:
Bài 42 trang 107 Sách bài tập Toán 9 Tập 2:
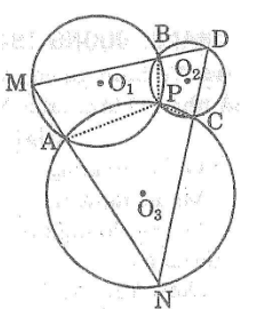
Cho ba đường tròn ùng đi qua một điểm P.Gọi các giao điểm khác P của hai trong ba đường tròn đó là A,B,C.Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB,DC cắt các đường tròn (PAB) ,(PAC) lần lượt tại M,N.Chứng minh ba điểm M,A,N thẳng hàng
Lời giải:
Gọi O1 , O2 ,O3 lần lượt là tâm của ba đường tròn
Ta có: (O1) cắt (O2) tại A, (O2) cắt (O3) tại C , (O3) cắt (O1) tại B
Suy ra: D là điểm nằm trên (O3)
DB cắt (O1) tại M, DC cắt (O2) tại N
Nối MA, NA, PA, PB, PC
*Tứ giác APBM nội tiếp trong đường tròn (O1) nên ta có:
Bài 43 trang 107 Sách bài tập Toán 9 Tập 2:
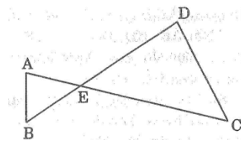
Cho đoạn thẳng AC và BD cắt nhau tại E
Biết AE.EC=BE.ED .Chứng minh bốn điểm A,B,C,D cùng nằm trên một đường tròn
Lời giải:
Ta có: AE.EC=BE.ED (gt)
Suy ra : AE/ED = BE/EC
Xét ΔABE và ΔDCE ta có:
AE/ED = BE/EC
Vì A và D nhìn đoạn BC cố định dưới một góc bằng nhau nên A và D nằm trên một cung chứa góc vẽ trên BC hay bốn điểm A ,B ,C ,D cùng nẳm trên một đường tròn