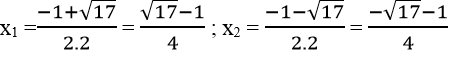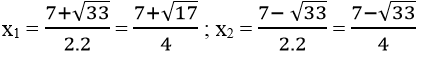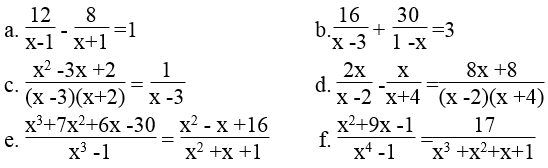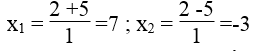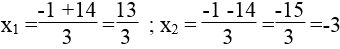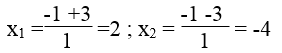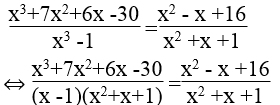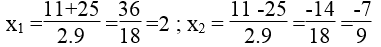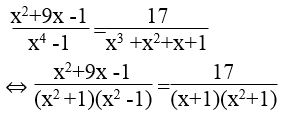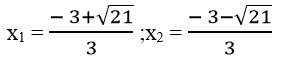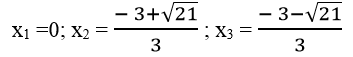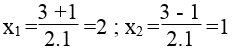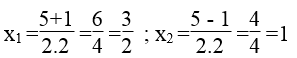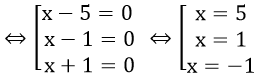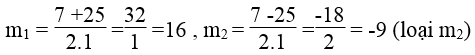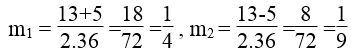Bài 7: Phương trình quy về phương trình bậc hai
Bài 45 trang 59 Sách bài tập Toán 9 Tập 2:
Giải các phương trình:
a. (x+2)2 -3x -5 =(1 –x)(1 +x)
b. (x -1)3 +2x=x3– x2 – 2x +1
c. x(x2 -6 ) – (x – 2)2 = (x +1)3
d. (x +5)2 + (x -2)2 + (x +7)(x -7) = 12x -23
Lời giải:
a) Ta có: (x+2)2 -3x -5 = (1 –x)(1 +x)
⇔ x2 + 4x +4 -3x -5 =1 – x2
⇔ 2x2 +x -2 =0
Δ = 12 -4.2.(-2) =1 +16 =17 > 0
√Δ = √17
b) Ta có: (x -1)3 +2x=x3 – x2 – 2x +1
⇔ x3 – 3x2 +3x -1+2x =x3 – x2 -2x +1
⇔ 2x2 – 7x +2 =0
Δ = (-7)2 -4.2.2 = 49 – 16 = 33 > 0
√Δ = √33
c) Ta có: x(x2 -6 ) – (x – 2)2 = (x +1)3
⇔ x3 – 6x – x2 +4x -4 =x3 + 3x2 +3x +1
⇔ 4x2 +5x +5 =0
Δ = 52 -4.4.5 = 25 – 80 = -55 < 0
Vậy phương trình vô nghiệm
d) Ta có: (x +5)2 + (x -2)2 + (x +7)(x -7) = 12x -23
⇔ x2 +10x + 25 +x2 -4x +4 +x2 -49 = 12x -23
⇔ x2 +10x+25 +x2 -4x +4 +x2 -49 -12x +23 =0
⇔ 3x2 -6x + 3 =0
⇔ x2 -2x +1 =0
Δ’ = (-1)2 -1.1 = 1-1 =0
Vậy phương trình đã cho có nghiệm kép: x1 = x2 =1
Bài 46 trang 59 Sách bài tập Toán 9 Tập 2:
Giải các phương trình:
Lời giải:
a. Điều kiện : x ≠ ± 1
Ta có: 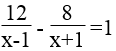
⇔ 12x +12 -8x +8 = x2 -1 ⇔ x2 -4x -21 =0
Δ’ = (-2)2 -1.(-21) = 4 + 21=25 > 0
√Δ’ =√25 =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x =7 và x =-3
b. Điều kiện : x ≠3 và x ≠ 1
Ta có: 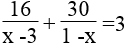
⇔ 16 – 16x +30x -90 =3x -3x2 -9 +9x
⇔ 3x2 +2x -65 =0
Δ’ = 12 -3.(-65) = 1 + 195=196 > 0
√Δ’ =√196 =14
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x =133 và x =-3
c.Điều kiện : x≠3 và x ≠ -2
Ta có: 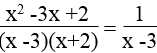
Phương trình x2 -4x +3 = 0 có a = 1 ,b = -4 , c = 3
Suy ra : a + b + c = 0
Ta có nghiệm x1 =1 , x2 =3 (loại)
Vậy nghiệm của phương trình là x =1
d. Điều kiện : x≠2 và x ≠ -4
Ta có: 
⇔ 2x2 +8x –x2 +2x =8x +8
⇔ x2 +2x -8 =0
Δ’ = 12 -1(-8) = 1 +8=9 > 0
√Δ’ =√9 =3
Cả hai giá trị của x đều không thỏa mãn điều kiện bài toán
Vậy phương trình đã cho vô nghiệm
e. Điều kiện : x≠1
Ta có:
⇔ x3+7x2 +6x -30 = (x2 –x +16)(x -1)
⇔ x3+7x2 +6x -30 = x3 – x2 – x2 +x +16x -16
⇔ 9x2 -11x -14 =0
Δ = (-11)2 -4.9.(-14) =121 +504 =625 > 0
√Δ =√625 =25
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x =-79 và x =2
f. Điều kiện : x≠ ± 1
ta có:
⇔ x2 +9x -1 =17x -17 ⇔ x2 -8x +16 =0
Δ’ = (-4)2 – 1.16=16 -16 =0
Phương trình có nghiệm kép 😡1 =x2 =4
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x =4
Bài 47 trang 59 Sách bài tập Toán 9 Tập 2:
Giải các phương trình sau bằng cách đưa về phương trình tích
a.3x3 +6x2 -4x =0 b.(x +1)3 –x +1 = (x -1)(x -2)
c.(x2 +x +1)2 = (4x -1 )2 d.(x2 +3x + 2)2 = 6.(x2 +3x +2)
e.(2x2 +3)2 -10x3 -15x =0 f.x3 – 5x2 –x +5 =0
Lời giải:
a) Ta có: 3x3 +6x2 -4x =0 ⇔ x(3x2 +6x -4) =0
⇔ x = 0 hoặc 3x2 +6x -4 =0
Giải phương trình 3x2 +6x -4 =0
Δ’ = 32 -3(-4) =9 +12 =21 > 0
√Δ’ =√21
Vậy phương trình đã cho có 3 nghiệm
b) Ta có: (x +1)3 –x +1 = (x -1)(x -2)
⇔ x3 +3x2+3x +1 –x +1 = x2 -2x –x +2
⇔ x3 +2x2 +5x = 0 ⇔ x(x2 +2x +5) =0
⇔ x =0 hoặc x2 +2x +5 =0
Giải phương trình x2 +2x +5 =0
Δ’ = 12 -1.5 =1 -5 = -4 < 0 ⇒ phương trình vô nghiệm
Vậy phương trình đã cho có 1 nghiệm : x=0
c) Ta có: (x2 +x +1)2 = (4x -1 )2
⇔ [(x2 +x +1) + (4x -1 )] [(x2 +x +1) – (4x -1 )]=0
⇔ (x2 +5x)(x2 -3x +2) =0 ⇔ x(x+5) (x2 -3x +2) =0
⇔ x =0 hoặc x+5 =0 hoặc x2 -3x +2 =0
x+5 =0 ⇔ x=-5
x2 -3x +2 =0
Δ = (-3)2 -4.2.1 = 9 -8 =1 > 0
√Δ =√1 =1
Vậy phương trình đã cho có 4 nghiệm:
x1 =0 ; x2 =-5 ; x3 =2 ; x4 =1
d) (x2 +3x + 2)2 = 6.(x2 +3x +2)
⇔ (x2 +3x + 2)2 – 6.(x2 +3x +2)=0
⇔ (x2 +3x + 2)[ (x2 +3x + 2) -6] =0
⇔ (x2 +3x + 2) .(x2 +3x -4 )=0
x2 +3x + 2 =0
Phương trình có dạng a –b +c =0 nên x1 = -1 ,x2 =-2
x2 +3x -4 =0
Phương trình có dạng a +b +c =0 nên x1 = 1 ,x2=-4
Vậy phương trình đã cho có 4 nghiệm :
x1 = -1 ,x2 =-2 ; x3 = 1 ,x4 =-4
e) Ta có: (2x2 +3)2 -10x3 -15x = 0 ⇔ (2x2 +3)2 – 5x(2x2 +3)=0
⇔ (2x2 +3)( 2x2 +3 – 5x) = 0 ⇔ (2x2 +3)( 2x2 – 5x +3)=0
Vì 2x2 ≥ 0 nên 2x2 +3 > 0
Suy ra : 2x2 – 5x +3=0
Δ = (-5)2 -4.2.3 =25 -24=1 > 0
√Δ =√1 =1
vậy phương trình đã cho có 2 nghiệm: x1 = 3/2 ; x2 = 1
f) Ta có: x3 – 5x2 –x +5 =0 ⇔ x2( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
Vậy phương trình đã cho có 3 nghiệm 😡1 = 5;x2 =1;x3=-1
Bài 48 trang 60 Sách bài tập Toán 9 Tập 2:
Giải các phương trình trùng phương
a. x4 -8x2 – 9 =0 b. y4 – 1,16y2 + 0,16 =0
c. z4 -7z2 – 144 =0 d. 36t4 – 13t2 +1 =0
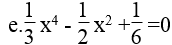
Lời giải:
a.Đặt m = x2 .Điều kiện m ≥ 0
Ta có: x4 -8x2 – 9 =0 ⇔m2 -8m -9 =0
Phương trìnhm2 – 8m – 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0
suy ra: m1 = -1 (loại) , m2 = -9/1 =9
Ta có: x2 =9 ⇒ x=± 3
Vậy phương trình đã cho có 2 nghiệm : x1 =3 ;x2 =-3
b. Đặt m = y2 .Điều kiện m ≥ 0
Ta có: y4 – 1,16y2 + 0,16 =0 ⇔m2 -1,16m + 0,16 =0
Phương trìnhm2 -1,16m + 0,16 = 0 có hệ số a = 1, b = -1,16, c = 0,16 nên có dạng a + b + c = 0
suy ra: m1 = 1 , m2 = 0,16
Ta có: y2 =1 ⇒ y = ± 1
y2 =0,16 ⇒ y = ± 0,4
Vậy phương trình đã cho có 4 nghiệm : y1 =1 ;y2 =-1 ; y3 =0,4 ;y4 =-0,4
c. Đặt m =z2 .Điều kiện m ≥ 0
Ta có: z4 -7z2 – 144 =0 ⇔m2 -7m -144 =0
Ta có: Δ=(-7)2 -4.1.(-144) =49 + 576=625 > 0
√Δ =√625 = 25
Ta có: z2 =16 ⇒ z=± 4
Vậy phương trình đã cho có 2 nghiệm : z1 =4 ;z2 =-4
d. Đặt m = t2 .Điều kiện m ≥ 0
Ta có: 36t4 – 13t2 +1 =0 ⇔ 36m2 -13m +1 =0
Ta có: Δ=(-13)2 – 4.36.1=169 -144=25 > 0
√Δ =√25 = 5
Ta có: t2 =1/4 ⇒ t=± 1/2
t2 =1/9 ⇒ t=± 1/3
Vậy phương trình đã cho có 4 nghiệm :
t1 = 1/4 ; t2 =-1/4 ; t3 =1/3 ; t4 =-1/3
e. Đặt m =x2 .Điều kiện m ≥ 0
Ta có: 1/3.(x4) – 1/2.( x2) +16 =0⇔ 2x4 -3x2 +1=0 ⇔ 2m2 -3m + 1 =0
Phương trình 2m2 -3m + 1 =0 có hệ số a=2,b=-3,c=1 nên có dạng a +b+c =0
suy ra: m1 = 1 , m2 = 12
Ta có: x2 = 1 ⇒ x = ± 1
x2 = 1/2 ⇒ x = ± √2/2
Vậy phương trình đã cho có 4 nghiệm :
x1 =1 ; x2 =-1 ; x3 =( √2)/2; x4 = – √2/2
f. Đặt m =x2 .Điều kiện m ≥ 0
Ta có: √3 x4 – (2 -√3 )x2 -2 =0 ⇔ √3m2 – (2 -√3 )m – 2 =0
Phương trình √3m2 – (2 -√3 )m – 2 =0 có hệ số a=√3 ,b= -(2 -√3 ),c=-2 nên có dạng a – b+c =0
Bài 49 trang 60 Sách bài tập Toán 9 Tập 2:
Chứng minh rằng khi a và c trái dấu thì phương trình trùng phương ax4+bx2+c =0 chỉ có hai nghiệm và chúng là hai số đối nhau
Lời giải:
Đặt m =x2 .Điều kiện m ≥ 0
Ta có: ax4 + bx2 + c = 0 ⇔ am2 + bm + c = 0
Vì a và c trái dấu nên a/c < 0. Phương trình có 2 nghiệm phân biệt là m1 và m2
Theo hệ thức Vi-ét,ta có: m1m2 = c/a
Vì a và c trái dấu nên c/a <0 suy ra m1m2 < 0 hay m1 và m2 trái dấu nhau
Vì m1 và m2 trái dấu nhau nên có 1 nghiệm bị loại ,giả sử loại m1
Khi đó x2 =m2 => x = ± √m2
Vậy phương trình trùng phương ax4+bx2+c =0 chỉ có hai nghiệm và chúng là hai số đối nhau khi a và c trái dấu
Bài 50 trang 60 Sách bài tập Toán 9 Tập 2:
Giải các phương trình sau bằng cách đặt ẩn số phụ
a.(4x -5)2 – 6(4x -5) +8 =0
b.(x2 +3x -1)2 +2(x2 +3x -1) -8 =0
c. (2x2 +x -2)2 +10x2 +5x -16 =0
d.(x2 -3x +4)(x2 -3x +2) =3
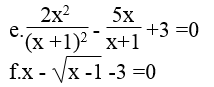
a) Đặt m =4x -5
Ta có: (4x -5)2– 6(4x -5) +8 =0 ⇔ m2 -6m +8 =0
Δ’ = (-3)2 -1.8 =9 -8=1 > 0
Δ’ =1 =1
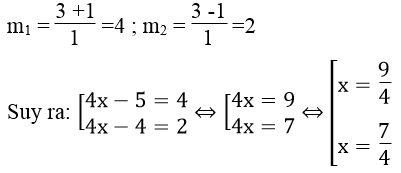
b) Đặt m = x2 +3x -1
Ta có: (x2 +3x -1)2 +2(x2 +3x -1) -8 =0 ⇔ m2 +2m -8 =0
Δ’ = 12 -1.(-8) =1 +8 =9 > 0
√Δ’ =√9 =3
m1 = -1 +31 =2 ; m2 = -1 -31 =-4
Với m = 2 thì : x2 +3x – 1 = 2 ⇔ x2 + 3x – 3 = 0
Δ’ = 32 -4.1.(-3 )=9 +12=21 > 0
√Δ =√21
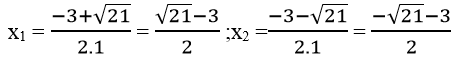
Δ = 32 -4.1.3=9 -12 = -3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
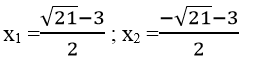
Ta có: (2x2 +x -2)2+10x2 +5x -16 =0
⇔ (2x2 +x -2)2+5(2x2 +x -2) -6 =0
⇔ m2 +5m -6 =0
Phương trình m2 +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng
a + b + c = 0
Suy ra : m1 =1 ,m2 =-6
m1 =1 ta có: 2x2 +x -2 =1 ⇔ 2x2 +x -3=0
Phương trình 2x2 +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng
a +b+c=0
Suy ra: x1 =1 ,x2 =-3/2
Với m=-6 ta có: 2x2 +x -2 = -6 ⇔ 2x2 +x +4 =0
Δ = 12 -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x1 =1 ,x2 =-32
d) Đặt m= x2 -3x +2
Ta có: (x2 -3x +4)(x2 -3x +2) =3
⇔ [(x2 -3x +2 +2)(x2 -3x +2) -3 =0
⇔ (x2 -3x +2)2 +2(x2 -3x +2) -3 =0
⇔ m2 +2m -3 =0
Phương trình m2 +2m -3 = 0 có hệ số a = 1, b = 2 , c = -3 nên có dạng
a +b+c=0
suy ra : m1 =1 ,m2 =-3
Với m1 =1 ta có: x2 -3x +2 =1 ⇔ x2 -3x +1=0
Δ = (-3)2 -4.1.1 = 9 -4 =5 > 0
√Δ = √5
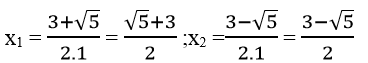
Δ = (-3)2 -4.1.5 = 9 -20 =-11 < 0.Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
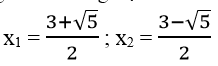
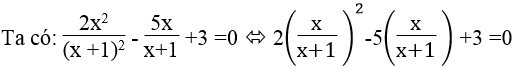
Phương trình 2m2 -5m +3 = 0 có hệ số a = 2, b = -5 , c = 3 nên có dạng
a +b + c = 0
suy ra : m1 = 1 ,m2 =3/2
Với m1 =1 ta có: x/(x+1) =1 ⇔ x =x+1 ⇔ 0x =1 (vô nghiệm)
Với m = 3/2 ta có: x/(x+1) = 3/2 ⇔ 2x =3(x +1)
⇔ 2x =3x +3 ⇔ x =-3
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=-3
f. Đặt m = √(x -1) .Điều kiện : x ≥ 0
Ta có : x – √(x -1)-3 =0 ⇔ (x -1) -√(x -1) -2 =0
⇔ m2 -m – 2 =0
Phương trình m2 -m – 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng
a – b + c = 0
Suy ra : m1 = -1 (loại) , m2 = -(-2)/1 = 2
Với m =2 ta có:√(x -1) =2 ⇒ x -1 =4 ⇔ x =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=5