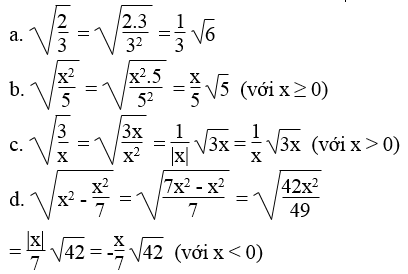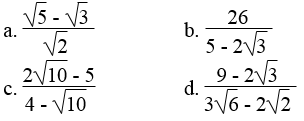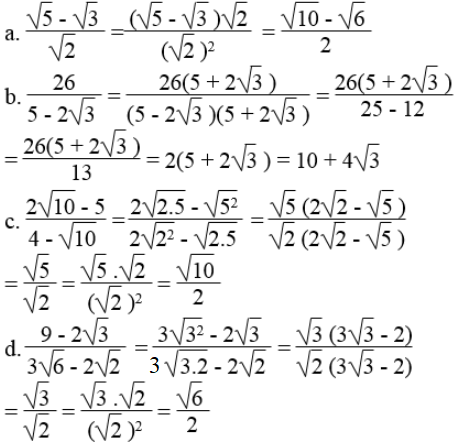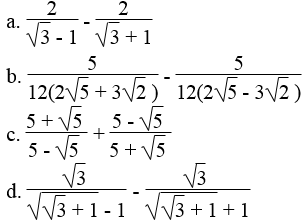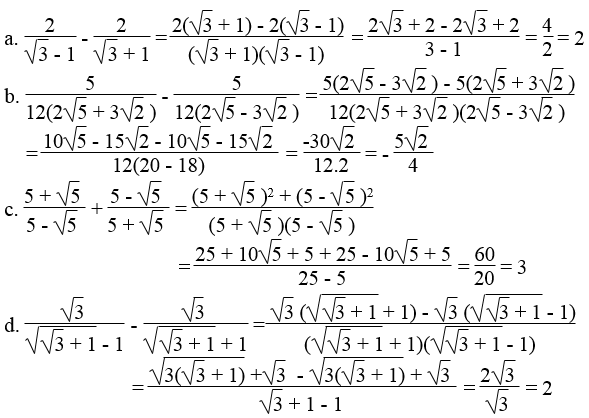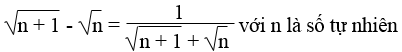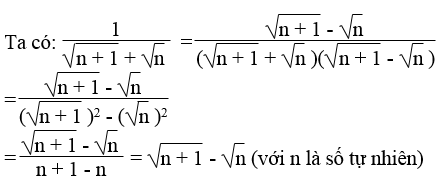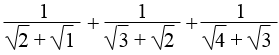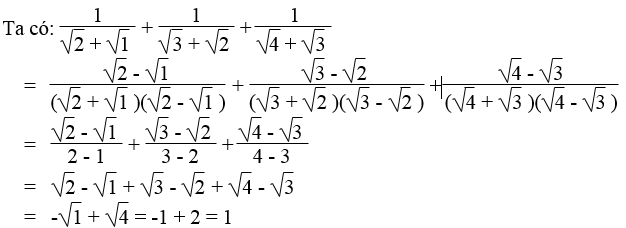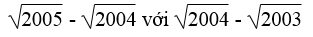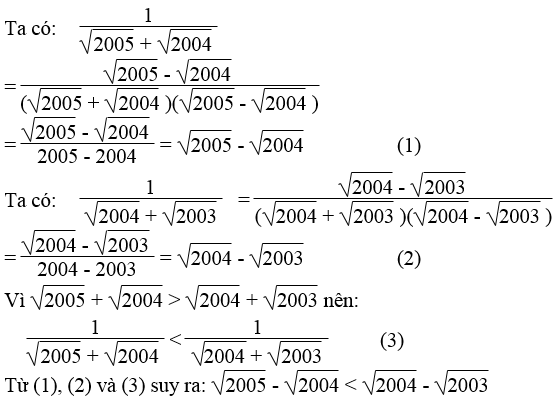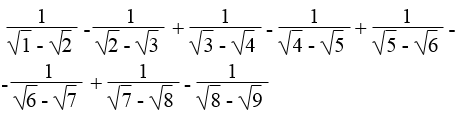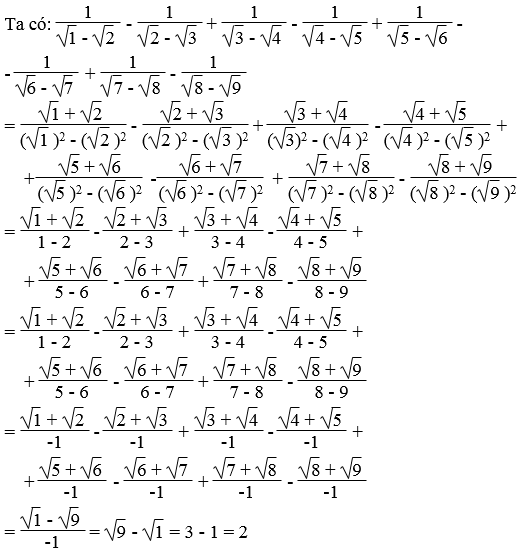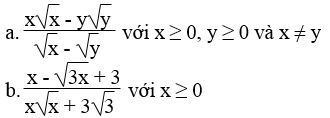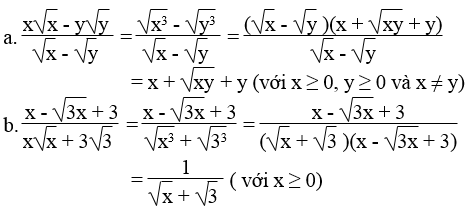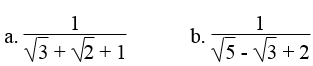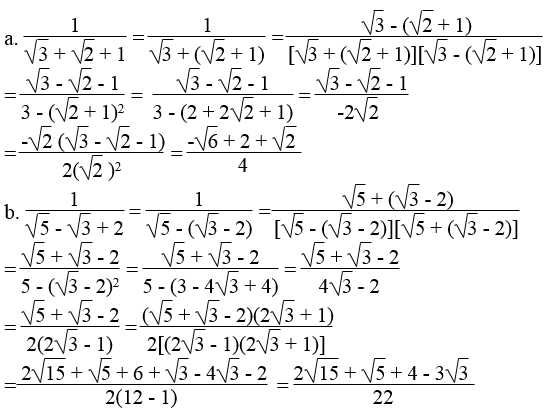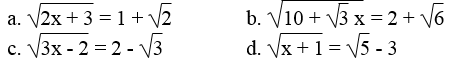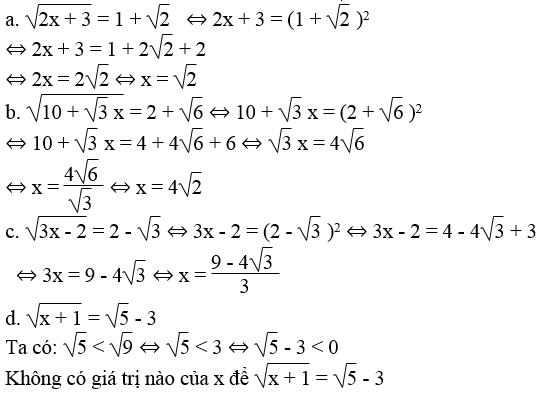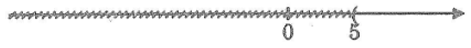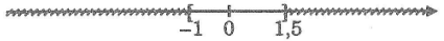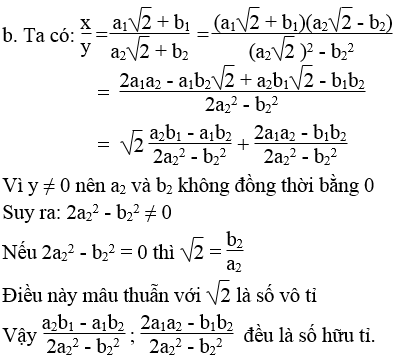Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài 68 trang 16 Sách bài tập Toán 9 Tập 1:
Khử mẫu của mỗi biểu thức lấy căn và rút gọn (nếu được):
Lời giải:
Bài 69 trang 16 Sách bài tập Toán 9 Tập 1:
Trục căn thức ở mẫu và rút gọn (nếu được):
Lời giải:
Bài 70 trang 16 Sách bài tập Toán 9 Tập 1:
Rút gọn các biểu thức:
Lời giải:
Bài 71 trang 16 Sách bài tập Toán 9 Tập 1:
Chứng minh đẳng thức:
Lời giải:
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Bài 72 trang 17 Sách bài tập Toán 9 Tập 1:
Xác định giá trị biểu thức sau theo cách thích hợp:
Lời giải:
Bài 73 trang 17 Sách bài tập Toán 9 Tập 1:
So sánh (không dùng bảng số hay máy tính bỏ túi):
Lời giải:
Bài 74 trang 17 Sách bài tập Toán 9 Tập 1:
Rút gọn:
Lời giải:
Bài 75 trang 17 Sách bài tập Toán 9 Tập 1:
Rút gọn các biểu thức:
Lời giải:
Bài 76 trang 17 Sách bài tập Toán 9 Tập 1:
Trục căn thức ở mẫu:
Lời giải:
Bài 77 trang 17 Sách bài tập Toán 9 Tập 1:
Tìm x, biết:
Lời giải:
Bài 78 trang 17 Sách bài tập Toán 9 Tập 1:
Tìm tập hợp các giá trị x thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số:
Lời giải:
a. Điều kiện: x – 2 ≥ 0 ⇔ x ≥ 2
Ta có: √(x – 2) ≥ √3 ⇔ x – 2 ≥ 3 ⇔ x ≥ 5
Giá trị x ≥ 5 thỏa mãn điều kiện.
b. Điều kiện: 3 – 2x ≥ 0 ⇔ 3 ≥ 2x ⇔ x ≤ 1,5
Ta có: √(3 – 2x) ≤ √5 ⇔ 3 – 2x ≤ 5 ⇔ -2x ≤ 2 ⇔ x ≥ -1
Kết hợp với điều kiện ta có: -1 ≤ x ≤ 1,5
Bài 79 trang 17 Sách bài tập Toán 9 Tập 1:
Cho các số x và y có dạng: x = a1√2 + b1 và y = a2√2 + b2, trong đó a1, a2, b1, b2 là các số hữu tỉ. Chứng minh:
a. x + y và x.y cũng có dạng a√2 + b với a và b là các số hữu tỉ
b. x/y với y ≠ 0 cũng có dạng a√2 + b với a và b là các số hữu tỉ.
Lời giải:
a. Ta có: x + y = (a1√2 + b1) + (a2√2 + b2) = (a1 + a2)√2 + (b1 + b2)
Vì a1, a2, b1, b2 là các số hữu tỉ nên a1 + a2, b1 + b2 cũng là số hữu tỉ.
Lại có: xy = (a1√2 + b1)(a2√2 + b2) = 2a1a2 + a1b2√2 + a2b1√2 + b1b2
= (a1b2 + a2b1)√2 + (2a1a2 + b1b2)
Vì a1, a2, b1, b2 là các số hữu tỉ nên a1b2 + a2b1, a1a2 + b1b2 cũng là các số hữu tỉ.