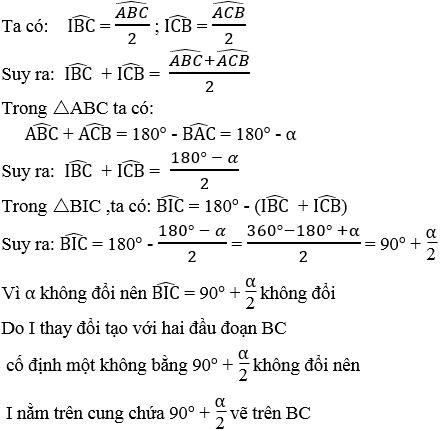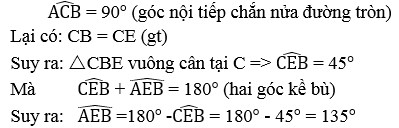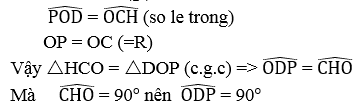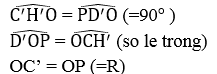Bài 6: Cung chứa góc
Bài 33 trang 105 Sách bài tập Toán 9 Tập 2:
Cho tam giác ABC có cạnh BC cố định và góc A = α không đổi.Tìm quỹ tích giao điểm của ba đường phân giác trong cuả tam giác
Lời giải:
*Chứng minh thuận:
Gọi I là giao điểm của ba đường phân giác trong của tam giác ABC
Bài 34 trang 105 Sách bài tập Toán 9 Tập 2:
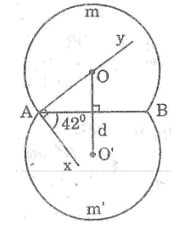
Dựng cung chứa góc 42° trên đoạn thẳng AB = 3cm
Lời giải:
– Dựng đoạn thẳng AB = 3cm
– Vẽ tia Ax sao cho góc (BAx) = 42°
– Dựng đường thẳng d là trung trực của đoạn AB
– Dựng tia Ay sao cho Ay ⊥ Ax (tia Ay cắt đường trung trực d của AB tại O)
– Dựng cung tròn AmB tâm O bán kính OA
– Dựng điểm O’ đối xứng với O qua AB
– Dựng cung tròn (Am’B) tâm O’ bán kính O’A
Ta được cung chứa 42° trên đoạn thẳng AB = 3cm
Bài 35 trang 106 Sách bài tập Toán 9 Tập 2:
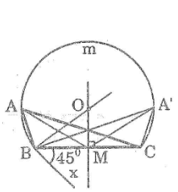
Dựng tam giác ABC biết BC = 3cm,góc A = 45° và trung tuyến AM = 2,5cm
Lời giải:
– Dựng đoạn thẳng AB = 3cm
– vẽ tia Bx sao cho góc (CBx) = 45°
– Dựng trung điểm M của BC
– Dựng đường trung trực của BC (qua M)
– Dựng tia vuông góc với Bx tại B ,cắt đường trung trực của BC tại O
– Dựng cung tròn BmC bán kính OB là cung chứa góc 45° vẽ trên đoạn BC
– Dựng cung tròn tâm M bán kính 2,5cm cắt cung BmC lần lượt tại A và A’
– Nối AB , AC (hoặc A’B , A’C) ta có: ΔABC (ΔA’BC) có BC = 3cm , góc A = 45°(hoặc góc (A’ ) =45°) và trung tuyến AM =2,5cm
Bài 36 trang 106 Sách bài tập Toán 9 Tập 2:
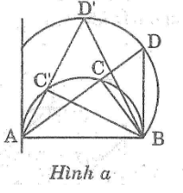
Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn trên dây AC kéo dài lấy điểm D sao cho CD=CB
a. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho
b. Trên tia CA lấy điểm E sao cho CE = CB.Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho
Lời giải:
Khi C chuyển động trên nửa đường tròn đường kính AB cố định thì C chuyển động trên cung chứa góc 45° dựng trên đoạn thẳng AB.Khi đó dây AC thay đổi phụ thuộc vào vị trí điểm C trên nửa đường tròn đường kính AB
– dây AC lớn nhất bằng đường kính của đường tròn .Khi C trùng với B thì D cũng trùng với B.vậy B là điểm của quỹ tích
– Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A.Khi đó D trùng với B’ là giao điểm của tiếp tuyến đường tròn đường kính AB tại A với cung chứa góc 45° vẽ trên AB
*Chứng minh đảo:
Lấy điểm D’ bất kì trên cung lớn AB ,nối AD’ cắt đường tròn đường kính AB tại C’.Nối BC’ ,B’D’
Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là cung BB’ nằm trên cung chứa góc 45° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C
b)
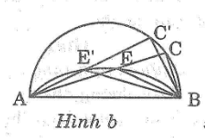
b. Hình b:
*chứng minh thuận
Trong đường tròn đường kính AB ta có:
Khi C chuyển động trên đường tròn đường kính AB cố định thì E chuyển động trên cung chứa góc 135° dựng trên đoạn thẳng AB cố định
-Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn thì C trùng với B nên E cũng trùng với B.vậy B là một điểm của quỹ tích
– Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A.khi đó E trùng với A nên A là một điểm của quỹ tích
Vậy E chuyển động trên cung chứa góc 135° vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C
*chứng minh đảo:
Lấy điểm E’ bất kì trên cung chứa góc 135° , nối AE’ cắt đường tròn đường kính AB tại C’.Nối BE’ ,B’C’
Quỹ tích điểm các điểm E khi C chuyển động trên nửa đường tròn đường kính AB là cung chứa góc 135° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C
Bài 37 trang 106 Sách bài tập Toán 9 Tập 2:
Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn .Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách CH từ C đến AB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho
Lời giải:
*Chứng minh thuận:
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P.
Vì O cố dịnh, đường tròn đường kính AB cố định nên P cố định.Nối PD
Ta có: OP // CH (cùng ⊥ AB)
Xét hai tam giác HCO và DOP ta có:
OD = CH (gt)
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với hai đầu đọa thẳng OP cố định một góc (ODP) = 90°
Vậy D chuyển động trên đường tròn đường kính OP
*Chứng minh đảo
Lấy điểm D’ bất kì trên đường tròn đường kính OP ,nối OD’ cắt nửa đường tròn đường kính AB tại C’.Nối PD’ và C’H’ ⊥ AB
Xét hai tam giác C’H’O và PD’O ta có:
Vậy ΔC’H’O = ΔPD’O (c.g.c) ⇒ C’H’ = OD’
Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP
Bài 38 trang 106 Sách bài tập Toán 9 Tập 2:
Dựng hình vuông ABCD ,biết đỉnh A , điểm M thuộc cạnh BC và điểm N thuộc cạnh CD
Lời giải:
– Dựng cung chứa góc 90° trên đoạn MN
– Dựng cung chứa góc 45° trên đoạn AM
Hai cung cắt nhau tại C
– Nối CM ,CN
– kẻ AB ⊥ CN tại B , AD ⊥ CN tại D
Tứ giác ABCD là hình vuông cần dựng