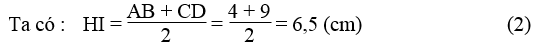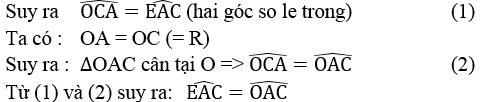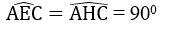Bài 4: Vị trí tương đối của đường thẳng và đường tròn
Bài 35 trang 162 Sách bài tập Toán 9 Tập 1:
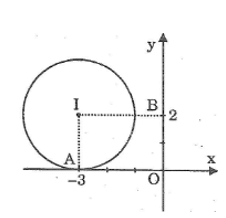
Trên mặt phẳng tọa độ cho điểm I có tọa độ (-3; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí như thế nào đối với các trục tọa độ?
Lời giải:
Kẻ IA ⊥ Ox
Ta có: IA = 2 = R
Suy ra đường tròn (I) tiếp xúc với trục hoành
Kẻ IB ⊥ Oy
Ta có : IB = 3 > R
Suy ra đường tròn và trục tung không có điểm chung
Bài 36 trang 162 Sách bài tập Toán 9 Tập 1:
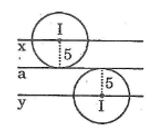
Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và tiếp xúc với đường thẳng a nằm trên đường nào ?
Lời giải:
Vì đường tròn tâm I bán kính 5cm tiếp xúc với đường thẳng a nên khoảng cách từ I đến a là 5cm.
Vậy I nằm trên hai đường thẳng x và y song song với a, cách a một khoảng bằng 5cm.
Bài 37 trang 162 Sách bài tập Toán 9 Tập 1:
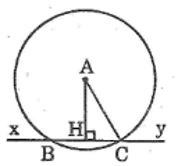
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm)
a. Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy
b. Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Lời giải:
a. Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C
b. Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
AC2 = AH2 + HC2
Suy ra: HC2 = AC2 – AH2 = 132 – 122 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)
Bài 38 trang 162 Sách bài tập Toán 9 Tập 1:
Cho đường tròn (O) bán kính bằng 2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB = BC. Kẻ đường kính COD. Tính độ dài AD.
Lời giải:
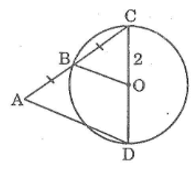
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD
Suy ra : OB = (1/2).AD (tính chất đường trung bình của tam giác)
Vậy AD = 2.OB = 2.2 = 4 (cm)
Bài 39 trang 162 Sách bài tập Toán 9 Tập 1:
Cho hình thang vuông ABCD có 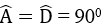
a. Tính độ dài AD
b. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính là BC
Lời giải:
a. Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
BC2 = BE2 + CE2
Suy ra : BE2 = BC2 – CE2 = 132 – 52 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)
b. Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD
Bài 40 trang 162 Sách bài tập Toán 9 Tập 1:
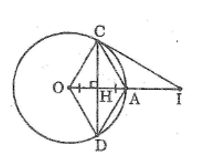
Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA.
a. Tứ giác OCAD là hình gì? Vì sao?
b. Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.
Lời giải:
a. Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Dồng thời CD ⊥ OA nên ACOD là hình thoi
b. Vì ACOD là hình thoi nên AC = OC
Mà OC = OA (= R) nên tam giác OAC đều
Bài 41 trang 162 Sách bài tập Toán 9 Tập 1:
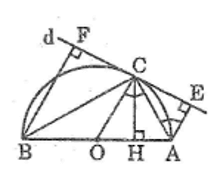
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng :
a. CE = CF
b. AC là tia phân giác của góc BAE
c. CH2 = AE.BF
Lời giải:
a. Ta có: OC ⊥ d (tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF (tính chất đường thẳng song song cách đều)
b. Ta có: AE // OC
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE
c. Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90o
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
CH2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ACH = ∆ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
CH = CF (= CE)
BC chung
Suy ra: ∆BCH = ∆BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: CH2 = AE.BF