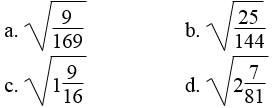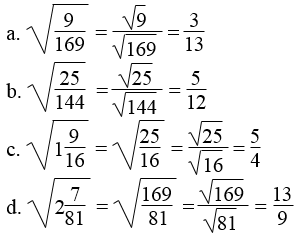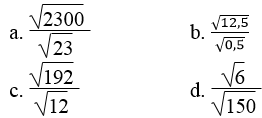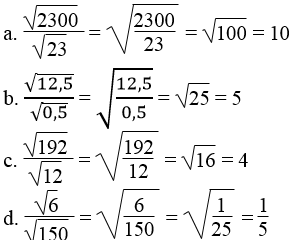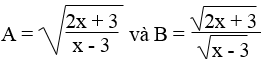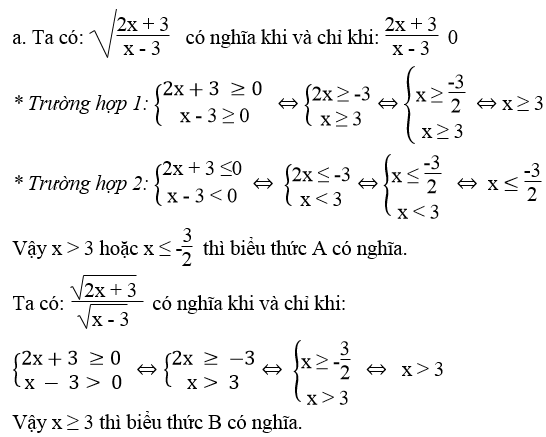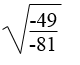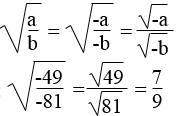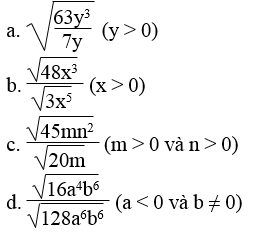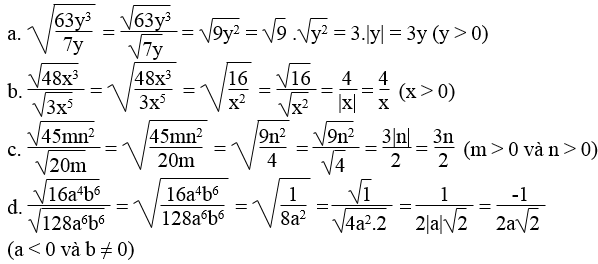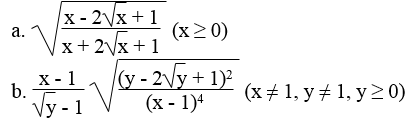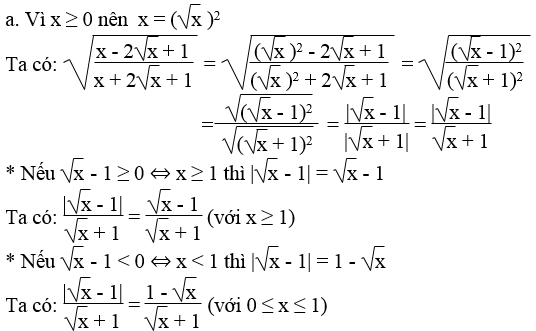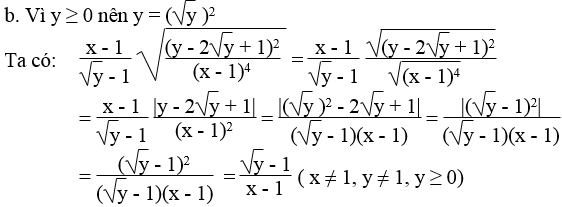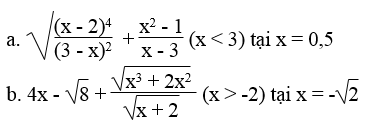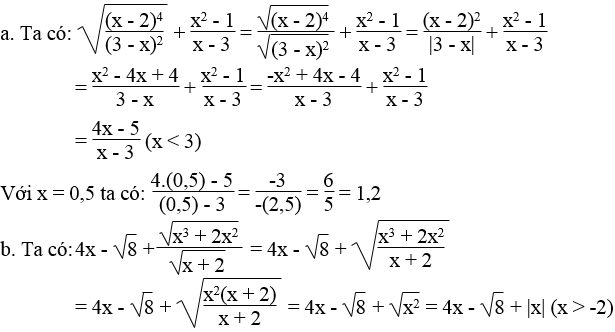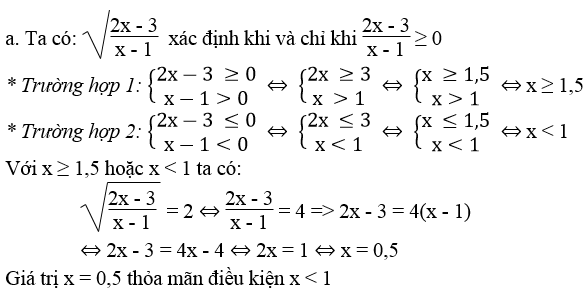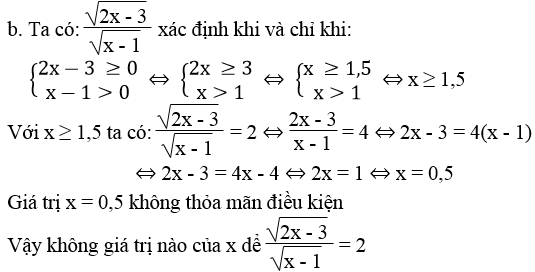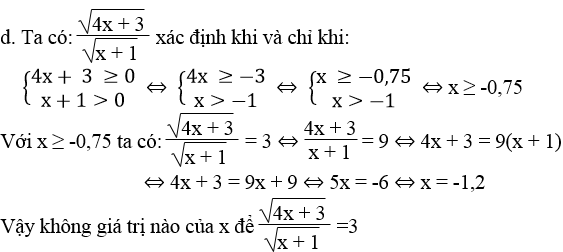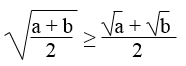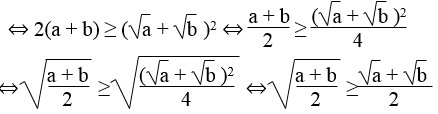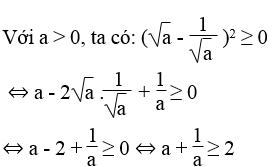Bài 4: Liên hệ giữa phép chia và phép khai phương
Bài 36 trang 10 Sách bài tập Toán 9 Tập 1:
Áp dụng quy tắc khai phương, hãy tính:
Lời giải:
Bài 37 trang 11 Sách bài tập Toán 9 Tập 1:
Áp dụng quy tắc chia hai căn bậc hai, hãy tính:
Lời giải:
Bài 38 trang 11 Sách bài tập Toán 9 Tập 1:
Cho các biểu thức:
a. Tìm x để A có nghĩa. Tìm x để B có nghĩa
b. Với giá trị nào của x thì A = B?
Lời giải:
b. Với x > 3 thì A và B đồng thời có nghĩa
Vậy với x > 3 thì A = B
Bài 39 trang 11 Sách bài tập Toán 9 Tập 1:
Biểu diễn 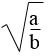
Áp dụng tính
Lời giải:
Ta có: a < 0 nên -a > 0; b < 0 nên -b > 0
Bài 40 trang 11 Sách bài tập Toán 9 Tập 1:
Rút gọn biểu thức:
Lời giải:
Bài 41 trang 11 Sách bài tập Toán 9 Tập 1:
Rút gọn các biểu thức:
Lời giải:
Bài 42 trang 12 Sách bài tập Toán 9 Tập 1:
Rút gọn biểu thức với điều kiện đã cho của x rồi tính giá trị của nó:
Lời giải:
* Nếu x > 0 thì |x| = x
Ta có: 4x – √8 + |x| = 4x – √8 +x = 5x – √8
Với x = -√2 ta có: 5(-√2 ) – 8 = -5√2 – 2√2 = -7√2
* Nếu -2 < x < 0 thì |x| = -x
Ta có: 4x – √8 + |x| = 4x – √8 – x = 3x – √8
Với x = -√2 ta có: 3(-√2 ) – √8 = -3√2 – 2√2 = -5√2
Bài 43 trang 12 Sách bài tập Toán 9 Tập 1:
Tìm x thỏa mãn điều kiện:
Lời giải:
Bài 44 trang 12 Sách bài tập Toán 9 Tập 1:
Cho hai số a, b, không âm. Chứng minh:
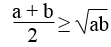
Dấu đẳng thức xảy ra khi nào?
Lời giải:
Vì a ≥ 0 nên √a xác định, b ≥ 0 nên √b xác định
Ta có: (√a – √b )2 ≥ 0 ⇔ a – 2√ab + b ≥ 0
⇔ a + b ≥ 2√ab ⇔
Dấu đẳng thức xảy ra khi a = b.
Bài 45 trang 12 Sách bài tập Toán 9 Tập 1:
Với a ≥ 0 và b ≥ 0, chứng minh
Lời giải:
Vì a ≥ 0 nên √a xác định, b ≥ 0 nên √b xác định
Ta có: (√a – √b )2 ≥ 0 ⇔ a – 2√ab + b ≥ 0 ⇔ a + b ≥ 2√ab
⇔ a + b + a + b ≥ a + b + 2√ab
⇔ 2(a + b) ≥ (√a )2 + 2√ab + (√b )2
Bài 46 trang 12 Sách bài tập Toán 9 Tập 1:
Với a dương, chứng minh a + 1/a ≥ 2
Lời giải: