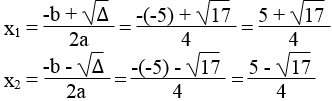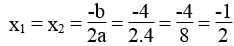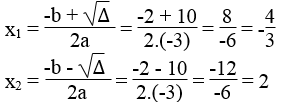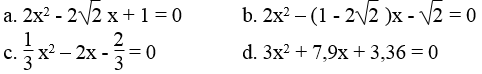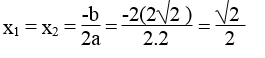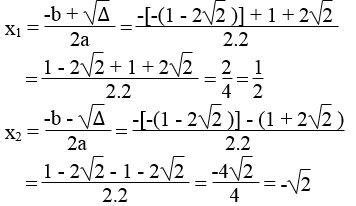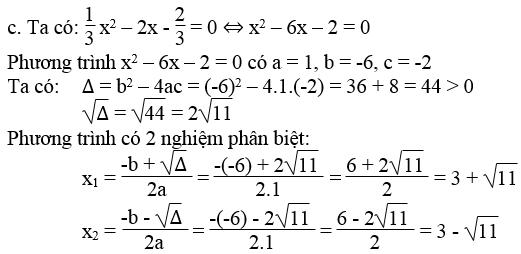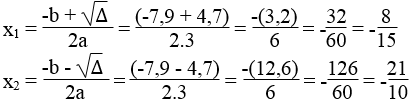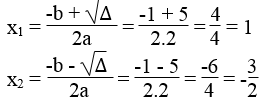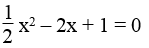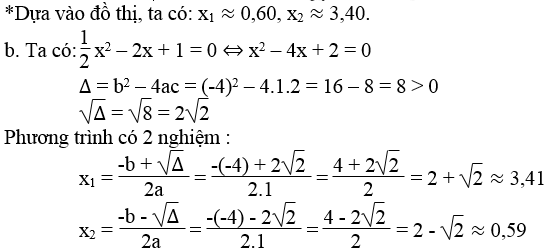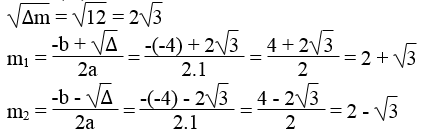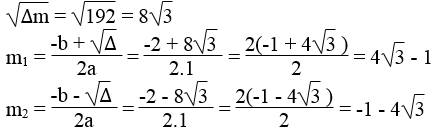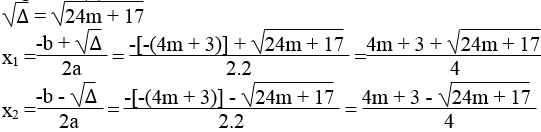Bài 4: Công thức nghiệm của phương trình bậc hai
Bài 20 trang 53 Sách bài tập Toán 9 Tập 2:
Xác định các hệ số a, b, c ; tính biệt thức ∆ rồi tìm nghiệm của các phương trình :
a. 2x2 – 5x + 1 = 0 b. 4x2 + 4x + 1 = 0
c. 5x2 – x + 2 = 0 d. -3x2 + 2x + 8 = 0
Lời giải:
a. Phương trình 2x2 – 5x + 1 = 0 có a = 2, b = -5, c = 1
Ta có: ∆ = b2 – 4ac = (-5)2 – 4.2.1 = 25 – 8 = 17 > 0
√∆ = √17
Phương trình có 2 nghiệm phân biệt :
b. Phương trình 4x2 + 4x + 1 = 0 có a = 4, b = 4, c = 1
Ta có: ∆ = b2 – 4ac = 42 – 4.4.1 = 16 – 16 = 0
Phương trình có nghiệm kép :
c. Phương trình 5x2 – x + 2 = 0 có a = 5, b = -1, c = 1
Ta có: ∆ = b2 – 4ac = (-1)2 – 4.5.2 = 1 – 40 = -39 < 0
Vậy phương trình vô nghiệm.
d. Phương trình -3x2 + 2x + 8 = 0 có a = -3, b = 2, c = 8
Ta có: ∆ = b2 – 4ac = 22 – 4.(-3).8 = 4 + 96 = 100 > 0
√∆ = √100 = 10
Phương trình có 2 nghiệm phân biệt :
Bài 21 trang 53 Sách bài tập Toán 9 Tập 2:
Xác định các hệ số a, b, c rồi giải phương trình :
Lời giải:
a. Phương trình 2×2 – 2√2 x + 1 = 0 có a = 2, b = -2√2 , c = 1
Ta có: ∆ = b2 – 4ac = (-2√2 )2 – 4.2.1 = 8 – 8 = 0
Phương trình có nghiệm kép :
b. Phương trình 2×2 – (1 – 2√2 )x – 2 = 0 có a = 2, b = -(1 – 2√2 ), c = -2
Ta có: ∆ = b2 – 4ac = [-(1 – 2√2 )]2 – 4.2.(-2 )
= 1 – 4√2 + 8 + 8√2 = 1 + 4√2 + 8
= 1 + 2.2√2 + (2√2 )2 = (1 + 2√2 )2 > 0
∆ = (1 + 2√2 )2 = 1 + 2√2
Phương trình có 2 nghiệm phân biệt :
d. Phương trình 3x2 + 7,9x + 3,36 = 0 có a = 3, b = 7,9, c = 3,36
Ta có: ∆ = b2 – 4ac = 7,92 – 4.3.3,36 = 62,41 – 40,32 = 22,09 > 0
√∆ = √22,09 = 4,7
Phương trình có 2 nghiệm phân biệt :
Bài 22 trang 53 Sách bài tập Toán 9 Tập 2:
Giải phương trình bằng đồ thị :
Cho phương trình 2x2 + x – 3 = 0.
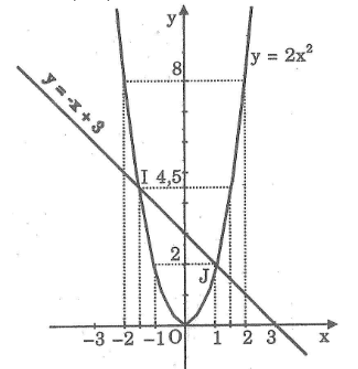
a. Vẽ các đồ thị của hai hàm số y = 2x2, y = -x + 3 trong cùng một mặt phẳng tọa độ.
b. Tìm hoành độ của mỗi giao điểm của hai đồ thị. Hãy giải thích vì sao các hoành độ này đều là nghiệm của phương trình đã cho.
c. Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu b.
Lời giải:
a. *Vẽ đồ thị hàm số y = 2x2
| x | -2 | -1 | 0 | 2 | 2 |
| y = 2x2 8 | 2 | 0 | 1 | 8 |
*Vẽ đồ thị hàm số y = -x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 3 ⇒ (3; 0)
b. Ta có: I(-1,5; 4,5), J(1; 2)
*x = -1,5 là nghiệm của phương trình 2x2 + x – 3 = 0 vì:
2(-1,5)2 + (-1,5) – 3 = 4,5 – 4,5 = 0
*x = 1 là nghiệm của phương trình 2x2 + x – 3 = 0 vì:
2.12 + 1 – 3 = 3 – 3 = 0
c. Ta có: ∆ = b2 – 4ac = 12 – 4.2.(-3) = 1 + 24 = 25 > 0
√∆ = √25 = 5
Phương trình có 2 nghiệm phân biệt :
Bài 23 trang 53 Sách bài tập Toán 9 Tập 2:
Cho phương trình
a. Vẽ các đồ thị của hai hàm sô 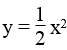
b. Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.
Lời giải:
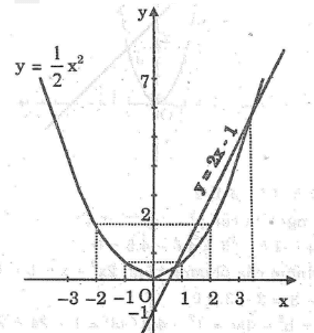
a. *Vẽ đồ thị hàm số
| x | -2 | -1 | 0 | 2 | 2 |
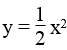 |
2 | 1/2 | 0 | 1/2 | 2 |
*Vẽ đồ thị hàm số y = 2x – 1
Cho x = 0 thì y = -1 ⇒ (0; -1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
Bài 24 trang 54 Sách bài tập Toán 9 Tập 2:
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm kép:
a. mx2– 2(m – 1)x + 2 = 0 b. 3x2 + (m + 1)x + 4 = 0
Lời giải:
a. Phương trình mx2 – 2(m – 1)x + 2 = 0 có nghiệm kép khi và chỉ khi m ≠ 0 và ∆ = 0
Ta có: ∆ = [-2(m – 1)]2 – 4.m.2 = 4(m2 – 2m + 1) – 8m
= 4(m2 – 4m + 1)
∆ = 0 ⇔ 4(m2 – 4m + 1) = 0 ⇔ m2 – 4m + 1 = 0
Giải phương trình m2 – 4m + 1. Ta có:
∆m = (-4)2 – 4.1.1 = 16 – 4 = 12 > 0
Vậy với m = 2 + √3 hoặc m = 2 – √3 thì phương trình đã cho có nghiệm kép.
b. Phương trình 3x2 + (m + 1)x + 4 = 0 có nghiệm kép khi và chỉ khi ∆ = 0
Ta có : ∆ = (m + 1)2 – 4.3.4 = m2 + 2m + 1 – 48 = m2 + 2m – 47
∆ = 0 ⇔ m2 + 2m – 47 = 0
Giải phương trình m2 + 2m – 47. Ta có:
∆m = 22 – 4.1.(-47) = 4 + 188 = 192 > 0
Vậy với m = 4√3 – 1 hoặc m = -1 – 4√3 thì phương trình đã cho có nghiệm kép.
Bài 25 trang 54 Sách bài tập Toán 9 Tập 2:
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m:
a. mx2 – (2m – 1)x + m + 2 = 0
b. 2x2 – (4m + 3)x + 2m2 – 1 = 0
Lời giải:
a. mx2 – (2m – 1)x + m + 2 = 0 (1)
*Nếu m = 0, ta có (1) ⇔ -x + 2 = 0 ⇔ x = 2
*Nếu m ≠ 0 thì (1) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có : ∆ = (2m – 1)2 – 4m(m + 2) = 4m2 – 4m + 1 – 4m2 – 8m
= -12m + 1
∆ ≥ 0 ⇔ -12m + 1 ≥ 0 ⇔ m ≤ 1/12
Vậy khi m ≤ 1/12 thì phương trình đã cho có nghiệm.
Giải phương trình (1) theo m :
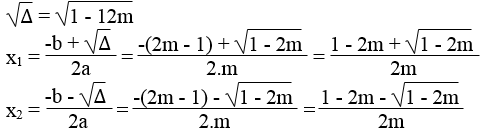
Phương trình (2) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có: ∆ = [-(4m + 3)]2 – 4.2(2m2 – 1)
= 16m2 + 24m + 9 – 16m2 + 8 = 24m + 17
∆ ≥ 0 ⇔ 24m + 17 ≥ 0 ⇔ m ≥ -17/24
Vậy khi m ≥ -17/24 thì phương trình đã cho có nghiệm.
Giải phương trình (2) theo m:
Bài 26 trang 54 Sách bài tập Toán 9 Tập 2:
Vì sao khi phương trình ax2 + bx + c = 0 có các hệ số a và c trái dấu thì nó có nghiệm?
Áp dụng: Không tính ∆, hãy giải thích vì sao mỗi phương trình sau có nghiệm:
a. 3x2– x – 8 = 0
b. 2004x2 + 2x – 1185√5 = 0
c. 3√2 x2 + (√3 – √2 )x + √2 – √3 = 0
d. 2010x2 + 5x – m2 = 0
Lời giải:
Khi a và c trái dấu thì ac < 0, suy ra –ac > 0, suy ra -4ac > 0
Ta có: ∆ = b2 – 4ac, trong đó b2 > 0
Nếu -4ac > 0 thì ∆ luôn lớn hơn 0.
Khi ∆ > 0 nghĩa là phương trình có hai nghiệm phân biệt.
Áp dụng :
a. Phương trình 3x2 – x – 8 = 0 có:
a = 3, c = -8 nên ac < 0
Vậy phương trình có 2 nghiệm phân biệt.
b. Phương trình 2004x2 + 2x – 1185√5 = 0 có:
a = 2004, c = -1185√5 nên ac < 0
Vậy phương trình có 2 nghiệm phân biệt.
c. Phương trình 3√2 x2 + (√3 – √2 )x + √2 – √3 = 0 có:
a = 3√2 , c = √2 – √3 nên ac < 0 (vì √2 < √3 )
Vậy phương trình có 2 nghiệm phân biệt.
d. 2010x2 + 5x – m2 = 0 (1)
*Với m = 0 thì (1) ⇔ 2010x2 + 5x = 0: phương trình có 2 nghiệm.
*Với m ≠ 0 ta có: m2 > 0, suy ra: -m2 < 0
Vì a = 2010 > 0, c = -m2 < 0 nên ac > 0
Vậy phương trình (1) có 2 nghiệm phân biệt.