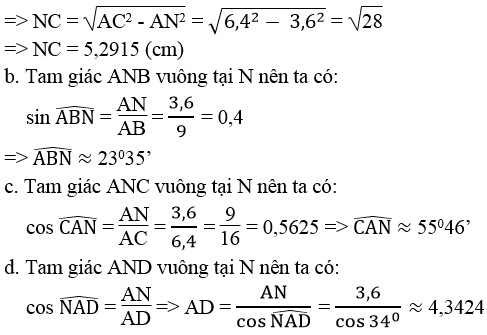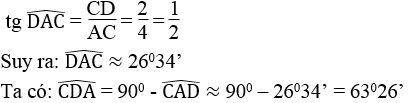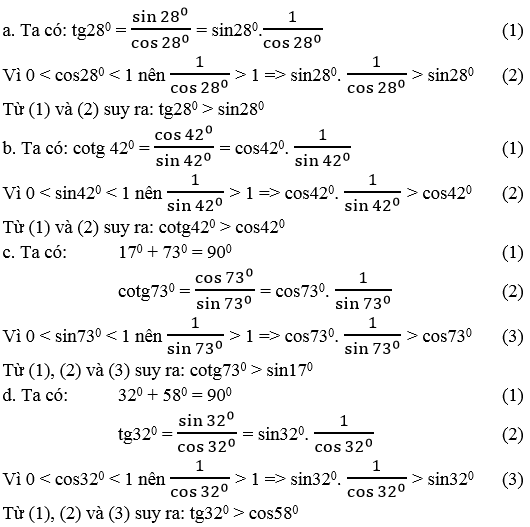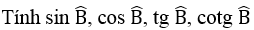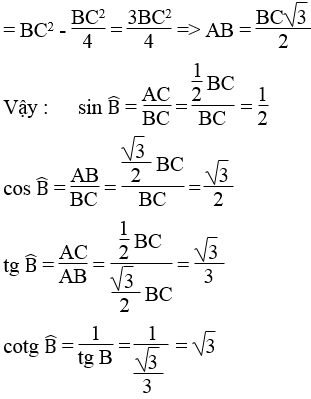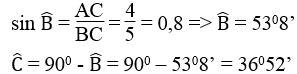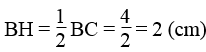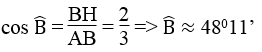Bài 3: Bảng lượng giác

Bài 39 trang 111 Sách bài tập Toán 9 Tập 1: 

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm: sin39^o13’; cos52^o18’; tg13^o20’; cotg10^o17’; sin45^o; cos45^o

Lời giải:

sin39^o13’ ≈ 0,6323     cos52^o18’ ≈ 0,6115

tg13^o20’ ≈ 0,2370     cotg10^o17’ ≈ 0,5118

sin45^o ≈ 0,7071     cos45^o ≈ 0,7071

 

 

Bài 40 trang 111 Sách bài tập Toán 9 Tập 1: 

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x:

a. sinx = 0,5446     b. cosx = 0,4444     c. tgx = 1,1111

Lời giải:

a. sinx = 0,5446 ⇒ x = 33^o

b. cosx = 0,4444 ⇒ x = 63^o47’

c. tgx = 1,1111 ⇒ x = 48^o

 

Bài 41 trang 111 Sách bài tập Toán 9 Tập 1:

 Có góc nhọn x nào mà:

a. sinx = 1,0100     b. cosx = 2,3540     c. tgx = 1,6754

Lời giải:

a. sinx = 1,0100: không có góc nhọn x vì sinx < 1

b. cosx = 2,3540: không có góc nhọn x vì cosx < 1

c. tgx = 1,6754 ⇒ x = 59^o10’

 

 

Bài 42 trang 111 Sách bài tập Toán 9 Tập 1:

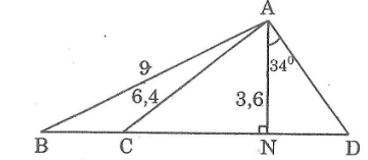
 Cho hình dưới, biết: AB = 9cm, AC = 6,4cm, AN = 3,6cm, 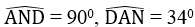 . Hãy tính:

a. CN     b. 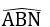     c.      d. AD

Lời giải:

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ANC, ta có:

AC² = AN² + NC² ⇒ NC² = AC² – AN²

 

 

Bài 43 trang 111 Sách bài tập Toán 9 Tập 1:

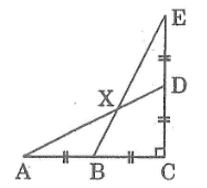
 Cho hình bên, biết: góc (ACE) = 90^o, AB = BC = CD = DE = 2cm. Hãy tính:

a. AD, BE

b. góc (DAC)

c. góc (BXD)

Lời giải:

a. Ta có:

AC = AB + BC = 2 + 2 = 4 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ACD, ta có:

AD² = AC² + CD² = 4² + 2² = 16 + 4 = 20

=> AD = √20 = 2√5 (cm)

Mặt khác: CE = CD + DE = 2 + 2 = 4 (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông BEC, ta có:

BE² = BC² + CE² = 2² + 4² = 4 + 16 = 20

=> BE = √20 = 2√5 (cm)

b. Tam giác ACD vuông tại C nên ta có:

Xét hai tam giác ACD và ECB, ta có:

AC = EC (= 4cm)

BC = DC (= 2 cm)

AD = EB (= 2√5 cm)

Suy ra: ∆ACD = ∆ECB (c.c.c)

 

 

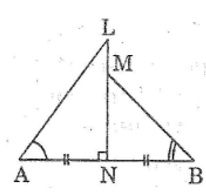
Bài 44 trang 112 Sách bài tập Toán 9 Tập 1:

 Đoạn thẳng LN vuông góc với đoạn thẳng AB tại trung điểm N của AB; M là một điểm của đoạn thẳng LN và khác với L, N. Hãy so sánh các góc (LAN) và góc (MBN) .

Lời giải:

 

Bài 45 trang 112 Sách bài tập Toán 9 Tập 1:

 Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh:

a. sin25^o và sin75^o     b. cos40^o và cos75^o

c. sin38^o và cos38^o     d. sin50^o và cos50^o

Lời giải:

a. Với 0^o < α < 90^o ta có α tăng thì sin α tăng

Ta có: 25^o < 75^o, suy ra sin25^o < sin75^o

b. Với 0^o < α < 90^o ta có α tăng thì cos α giảm

Ta có: 40^o < 75^o, suy ra cos45^o > cos75^o

c. Với 0^o < α < 90^o ta có α tăng thì sin α tăng

Ta có: 38^o + 52^o = 90^o, suy ra: cos38^o = sin52^o

Vì 38^o < 52^o nên sin38^o < sin52^o hay sin38^o < cos38^o

d. Với 0^o < α < 90^o ta có α tăng thì cos α giảm

Ta có: 40^o + 50^o = 90^o, suy ra: sin50^o = cos40^o

Vì 40^o < 50^o nên cos40^o > cos50^o hay sin50^o > cos50^o

Bài 48 trang 112 Sách bài tập Toán 9 Tập 1: 

Cho x là một góc nhọn, biểu thức sau đây có giá trị âm hay dương? Vì sao?

a. sinx – 1     b. 1 – cosx

c. sinx – cosx     d. tgx – cotgx

Lời giải:

a. Ta có: với 0^o < x < 90^o thì sinx < 1, suy ra sinx – 1 < 0

b. Ta có: với 0^o < x < 90^o thì cosx < 1, suy ra 1 – cosx > 0

c. Ta có: *nếu x = 45^o thì sinx = cosx, suy ra: sinx – cosx = 0

*nếu x < 45^o thì cosx = sin(90^o – x)

Vì x < 45^o nên 90^o – x > 45^o, suy ra: sinx < sin(90^o – x)

Vậy sinx – cosx < 0

*nếu x > 45^o thì cosx = sin(90^o – x)

Vì x > 45^o nên 90^o – x < 45^o, suy ra: sinx > sin(90^o – x)

Vậy sinx – cosx > 0.

d. Ta có: *nếu x = 45^o thì tgx = cotgx, suy ra: tgx – cotgx = 0

*nếu x < 45^o thì cotgx = tg(90^o – x)

Vì x < 45^o nên 90^o – x > 45^o, suy ra: tgx < tg(90^o – x)

Vậy tgx – cotgx < 0

*nếu x > 45^o thì cotgx = tg(90^o – x)

Vì x > 45^o nên 90^o – x < 45^o, suy ra: tgx > tg(90^o – x)

Vậy tgx – cotgx > 0.

 

 

Bài 47 trang 112 Sách bài tập Toán 9 Tập 1: 

Cho x là một góc nhọn, biểu thức sau đây có giá trị âm hay dương? Vì sao?

a. sinx – 1     b. 1 – cosx

c. sinx – cosx     d. tgx – cotgx

Lời giải:

a. Ta có: với 0^o < x < 90^o thì sinx < 1, suy ra sinx – 1 < 0

b. Ta có: với 0^o < x < 90^o thì cosx < 1, suy ra 1 – cosx > 0

c. Ta có: *nếu x = 45^o thì sinx = cosx, suy ra: sinx – cosx = 0

*nếu x < 45^o thì cosx = sin(90^o – x)

Vì x < 45^o nên 90^o – x > 45^o, suy ra: sinx < sin(90^o – x)

Vậy sinx – cosx < 0

*nếu x > 45^o thì cosx = sin(90^o – x)

Vì x > 45^o nên 90^o – x < 45^o, suy ra: sinx > sin(90^o – x)

Vậy sinx – cosx > 0.

d. Ta có: *nếu x = 45^o thì tgx = cotgx, suy ra: tgx – cotgx = 0

*nếu x < 45^o thì cotgx = tg(90^o – x)

Vì x < 45^o nên 90^o – x > 45^o, suy ra: tgx < tg(90^o – x)

Vậy tgx – cotgx < 0

*nếu x > 45^o thì cotgx = tg(90^o – x)

Vì x > 45^o nên 90^o – x < 45^o, suy ra: tgx > tg(90^o – x)

Vậy tgx – cotgx > 0.

 

Bài 48 trang 112 Sách bài tập Toán 9 Tập 1:

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh:

a. tg28^o và sin28^o     b. cotg42^o và cos42^o

c. cotg73^o và sin17^o     d. tg32^o và cos58^o

Lời giải:

 

 

Bài 49 trang 112 Sách bài tập Toán 9 Tập 1: 

Tam giác ABC vuông tại A, có AC = (1/2).BC.

Lời giải:

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

BC²= AB² + AC²

⇒AB² = BC² – AC²

 

 

Bài 50 trang 112 Sách bài tập Toán 9 Tập 1:

 Tính các góc của tam giác ABC, biết AB = 3cm, AC = 4cm và BC = 5cm

Lời giải:

Ta có: AB = 3 ⇒ AB² = 3² = 9

AC = 4 ⇒ AC² = 4² = 16

BC = 5 ⇒ BC² = 5² = 25

Ta có: AB² + AC² = 9 + 16 = 25 = BC2

Suy ra tam giác ABC vuông tại A.

Ta có:

 

 

Bài 51 trang 112 Sách bài tập Toán 9 Tập 1:

 Để vẽ một tam giác cân có góc ở đáy 50^o mà không có thước đo góc, một học sinh vẽ một tam giác cân có cạnh bên là 3cm, cạnh đáy 4cm. Tính góc ở đáy mà em học sinh đó đã vẽ. Sai số so với số đo phải vẽ là bao nhiêu?

Lời giải:

Giả sử tam giác ABC có AB = AC = 3cm, BC = 4cm.

Kẻ AH ⊥ BC. Ta có :

Tam giác ABH vuông tại H nên ta có:

Sai số là: 50^o – 48^o11’ = 1^o49’