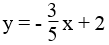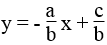Bài 1: Phương trình bậc nhất hai ẩn
Bài 1 trang 5 Sách bài tập Toán 9 Tập 2:
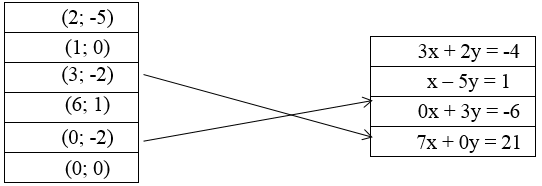
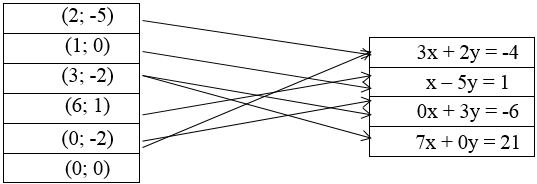
Cho các cặp số và các phương trình sau.
Hãy dùng mũi tên (như trong hình vẽ) chỉ rõ mỗi cặp số là nghiệm của những phương trình nào?
Lời giải:
Bài 2 trang 5 Sách bài tập Toán 9 Tập 2:
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
a. 2x – y = 3; b. x + 2y = 4;
c. 3x – 2y = 6; d. 2x + 3y = 5;
e. 0x + 5y = -10; f. -4x + 0y = -12.
Lời giải:
a. 2x – y = 3 ⇔ y = 2x – 3
Công thức nghiệm tổng quát (x ∈ R; y = 2x – 3}
b. x + 2y = 4 ⇔ 2y = -x + 4 ⇔
Công thức nghiệm tổng quát (x ∈ R; 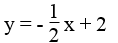
c. 3x – 2y = 6 ⇔ 2y = 3x – 6 ⇔
Công thức nghiệm tổng quát (x ∈ R; 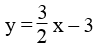
d. 2x + 3y = 5 ⇔ 3y = -2x + 5 ⇔
Công thức nghiệm tổng quát (x ∈ R; 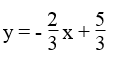
e. 0x + 5y = -10 ⇔ 5y = -10 ⇔ y = -2
Công thức nghiệm tổng quát (x ∈ R; y = -2)
f. -4x + 0y = -12 ⇔ -4x = -12 ⇔ x = 3
Công thức nghiệm tổng quát (x = 3; y ∈ R).
Bài 3 trang 5 Sách bài tập Toán 9 Tập 2:
Trong mỗi trường hợp sau, hãy tìm giá trị của m để:
a. Điểm M(1; 0) thuộc đường thẳng mx – 5y = 7;
b. Điểm N(0; -3) thuộc đường thẳng 2,5x + my = -21;
c. Điểm P(5; -3) thuộc đường thẳng mx + 2y = -1;
d. Điểm P(5; -3) thuộc đường thẳng 3x – my = 6;
e. Điểm Q(0,5; -3) thuộc đường thẳng mx – 0y = 17,5;
f. Điểm S(4; 0,3) thuộc đường thẳng 0x + my = 1,5;
g. Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m +1.
Lời giải:
a. Điểm M(1; 0) thuộc đường thẳng mx – 5y = 7 nên tọa độ của M phải nghiệm đúng phương trình đường thẳng.
Khi đó: m.1 – 5.0 = 7 ⇔ m = 7
Vậy với m = 7 thì đường thẳng mx – 5y = 7 đi qua M(1; 0)
b. Điểm N(0; -3) thuộc đường thẳng 2,5x + my = -21 nên tọa độ của N phải nghiệm đúng phương trình đường thẳng.
Khi đó: 2,5.0 + m(-3) = -21 ⇔ m = 7
Vậy với m = 7 thì đường thẳng 2,5x + my = -21 đi qua N(0; -3)
c. Điểm P(5; -3) thuộc đường thẳng mx + 2y = -1 nên tọa độ của P phải nghiệm đúng phương trình đường thẳng.
Khi đó: m.5 + 2.(3) = -1 ⇔ m = 1
Vậy với m = 1 thì đường thẳng mx + 2y = -1 đi qua P(5; -3)
d. Điểm P(5; -3) thuộc đường thẳng 3x – my = 6 nên tọa độ của P phải nghiệm đúng phương trình đường thẳng.
Khi đó: 3.5 – m.(-3) = 6 ⇔ m = -3
Vậy với m = -3 thì đường thẳng 3x – my = 6 đi qua P(5; -3)
e. Điểm Q(0,5; -3) thuộc đường thẳng mx – 0y = 17,5 nên tọa độ của Q phải nghiệm đúng phương trình đường thẳng.
Khi đó: m.0,5 + 0.(-3) = 17,5 ⇔ m = 35
Vậy với m = 35 thì đường thẳng mx – 0y = 17,5 đi qua Q(0,5; -3)
f. Điểm S(4; 0,3) thuộc đường thẳng 0x + my = 1,5 nên tọa độ của S phải nghiệm đúng phương trình đường thẳng.
Khi đó: 0.4 + m.0,3 = 1,5 ⇔ m = 5
Vậy với m = 5 thì đường thẳng mx + my = 1,5 đi qua S(4; 0,3)
g. Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m +1 nên tọa độ của A phải nghiệm đúng phương trình đường thẳng.
Khi đó ta có: (m – 1).2 + (m + 1).(-3) = 2m + 1
⇔ 2m – 2 – 3m – 3 = 2m + 1 ⇔ 3m + 6 = 0 ⇔ m = -2
Vậy với m = -2 thì đường thẳng (m – 1)x + (m + 1)y = 2m + 1 đi qua A(2; -3).
Bài 4 trang 6 Sách bài tập Toán 9 Tập 2:
Phương trình nào sau đây xác định một hàm số dạng y = ax + b.
a. 5x – y = 7; b. 3x + 5y = 10;
c. 0x + 3y = -1; d. 6x – 0y = 18.
Lời giải:
a. Ta có: 5x – y = 7 ⇔ y = 5x – 7
Xác định hàm số dạng y = ax + b với a = 5, b = -7
b. Ta có: 3x + 5y = 10 ⇔ 5y = -3x + 10 ⇔
Xác định hàm số dạng y = ax + b với a = – 3/5 , b = 2.
c. Ta có: 0x + 3y = -1 ⇔ 3y = -1 ⇔ y = – 1/3
Xác định hàm số dạng y = ax + b với a = 0, b = – 1/3
d. Ta có: 6x – 0y = 18 ⇔ 6x = 18 ⇔ x = 3
Phương trình không thuộc dạng y = ax + b.
Bài 5 trang 6 Sách bài tập Toán 9 Tập 2:
Phải chọn a và b như thế nào để phương trình ax + by = c xác định một hàm số bậc nhất của biến x?
Lời giải:
Ta có: ax + by = c ⇔
Để phương trình ax + by = c xác định một hàm số bậc nhất của biến x thì a ≠ 0 và b ≠ 0.
Bài 6 trang 6 Sách bài tập Toán 9 Tập 2:
Vẽ mỗi cặp đường thẳng sau trong cùng một mặt phẳng tọa độ rồi tìm tọa độ giao điểm của hai đường thẳng đó.
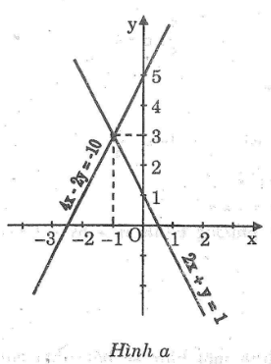
a. 2x + y = 1 và 4x – 2y = -10;
b. 0,5x + 0,25y = 0,15 và
c. 4x + 5y = 20 và 0,8x + y = 4;
d. 4x + 5y = 20 và 2x + 2,5y = 5.
Lời giải:
a. *Ta có: 2x + y = 1 ⇔ y = -2x + 1
Cho x = 0 thì y = 1 ⇒ (0; 1)
Cho y = 0 thì x = 1/2 ⇒ (1/2 ; 0)
*Ta có: 4x – 2y = -10 ⇔ y = 2x + 5
Cho x = 0 thì y = 5 ⇒ (0; 5)
Cho y = 0 thì x = – 5/2 ⇒ (- 5/2 ; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 1 = 2x + 5 ⇔ 4x = -4 ⇔ x = -1
Tung độ giao điểm của hai đường thẳng:
y = -2(-1) + 1 = 2 + 1 = 3
Vậy tọa độ giao điểm của hai đường thẳng là (-1; 3).
Đồ thị: hình a.
b. *Ta có: 0,5x + 0,25y = 0,15 ⇔ y = -2x + 0,6
Cho x = 0 thì y = 0,6 ⇒ (0; 0,6)
Cho y = 0 thì x = 0,3 ⇒ (0,3; 0)
*Ta có: 
Cho x = 0 thì y = -9 ⇒ (0; -9)
Cho y = 0 thì x = 3 ⇒ (3; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 0,6 = 3x – 9 ⇔ 5x = 9,6 ⇔ x = 1,92
Tung độ giao điểm của hai đường thẳng:
y = 3.1,92 – 9 = -3,24
Vậy tọa độ giao điểm của hai đường thẳng là (1,92; -3,24)
Đồ thị: hình b.
c. *Ta có: 4x + 5y = 20 ⇔ y = -0,8x + 4
Cho x = 0 thì y = 4 ⇒ (0; 4)
Cho y = 0 thì x = 5 ⇒ (5; 0)
*Ta có: 0,8x + y = 4 ⇔ y = 0,8x + 4
Vậy hai đường thẳng trùng nhau nên chúng có vô số điểm chung.
Đồ thị: hình c.
d. *Ta có: 4x + 5y = 20 ⇔ y = -0,8 + 4
Cho x = 0 thì y = 4 ⇒ (0; 4)
Cho y = 0 thì x = 5 ⇒ (5; 0)
*Ta có: 2x – 2,5y = 5 ⇔ y = -0,8x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2,5 ⇒ (2,5; 0)
Hai đường thẳng có hệ số góc bằng nhau nhưng tung độ khác nhau nên chúng song song với nhau. Suy ra chúng không có tọa độ giao điểm.
Đồ thị: hình d.
Bài 7 trang 6 Sách bài tập Toán 9 Tập 2:
Giải thích vì sao khi M(xo; yo) là giao điểm của hai đường thẳng: ax + by = c và a’x + b’y = c’ thì (xo; yo) là nghiệm chung của hai phương trình ấy.
Lời giải:
Vì M(xo; yo) thuộc đường thẳng ax + by = c nên tọa độ của nó nghiệm đúng phương trình đường thẳng này.
Ta có: axo + byo = c.
Vì M(xo; yo) thuộc đường thẳng a’x + b’y = c’ nên tọa độ của nó nghiệm đúng phương trình đường thẳng này.
Ta có: a’xo + b’yo = c’.
Vậy (xo; yo) là nghiệm chung của hai phương trình đường thẳng:
ax + by = c và a’x + b’y = c’.