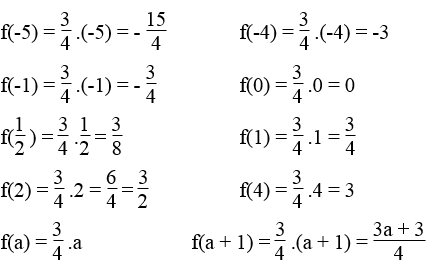Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
Bài 1 trang 60 Sách bài tập Toán 9 Tập 1:
Trong các bảng sau ghi các giá trị tương ứng của x và y. Bảng nào xác định y là hàm số của x? Vì sao?
a)
| x | 1 | 2 | 4 | 5 | 7 | 8 |
| y | 3 | 5 | 9 | 11 | 15 | 17 |
b)
| x | 3 | 4 | 3 | 5 | 8 |
| y | 6 | 8 | 4 | 8 | 16 |
Lời giải:
Bảng a) xác định y là hàm số của biến số x vì với mỗi giá trị của x ta xác định được một giá trị tương ứng duy nhất của y.
Bảng b) xác định y không phải là hàm số của biến số x vì với mỗi giá trị của x ta xác định được hai giá trị khác nhau của y.
Vì dụ x = 3 thì y = 6 và y = 4.
Bài 2 trang 60 Sách bài tập Toán 9 Tập 1:
Cho hàm số y = f(x) = 1,2x
Tính các giá trị tương ứng của y khi cho x các giá trị sau đây, rồi lập bảng các giá trị tương ứng giữa x và y:
| -2,5 | -2,25 | -2 | -1,75 | -1,5 | -1,25 | -1 |
| -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 |
| 1 | 1,25 | 1,5 1,75 | 2 | 2,25 | 2,5 |
Lời giải:
| x | -2,5 | -2,25 | -2 | -1,75 | -1,5 | -1,25 | -1 |
| y = f(x) = 1,2x | -3 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| x | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 |
| y = f(x) = 1,2x | -0,9 | -0,6 | -0,3 | 0 | 0,3 | 0,6 | 0,9 |
| x | 1 | 1,25 | 1,5 | 1,75 | 2 | 2,25 | 2,5 |
| y = f(x) = 1,2x | 1,2 | 1,5 | 1,8 | 2,1 | 2,4 | 2,7 | 3 |
Bài 3 trang 60 Sách bài tập Toán 9 Tập 1:
Cho hàm số y = f(x) =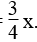 
. Tính:
| f(-5) | f(-4) | f(-1) | f(0) | f(1/2 ) |
| f(1) | f(2) | f(4) | f(a) | f(a + 1) |
Lời giải:
Bài 4 trang 60 Sách bài tập Toán 9 Tập 1:
Cho hàm số y = f(x) =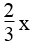 
+ 5 với x ∈R. Chứng minh rằng hàm số đồng biến trên R.
Lời giải:
Bài 5 trang 61 Sách bài tập Toán 9 Tập 1:
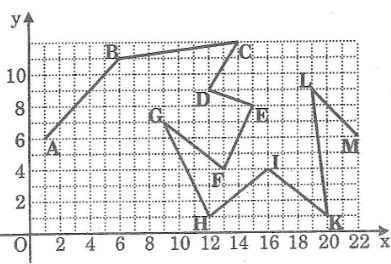
Biểu diễn các điểm sau đây trên cùng một hệ trục tọa độ. Nối theo thứ tự các điểm đã cho bằng các đoạn thẳng để được một đường gấp khúc với điểm đầu là A, điểm cuối là M.
| A(1; 6) | B(6; 11) | C(14; 12) |
| D(12; 9) | E(15; 8) | F(13; 4) |
| G(9; 7) | H(12; 1) | I(16; 4) |
| K(20; 1) | L(19; 9) | M(22; 6) |
Lời giải:
