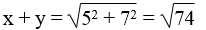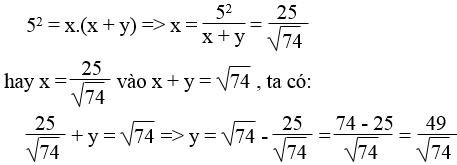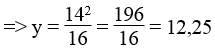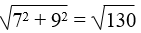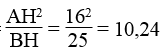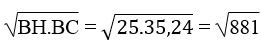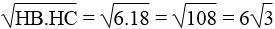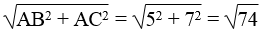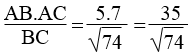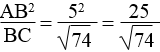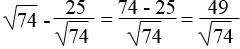Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Bài 1 trang 102 Sách bài tập Toán 9 Tập 1:
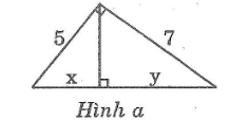
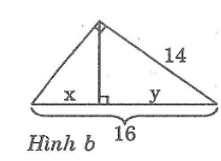
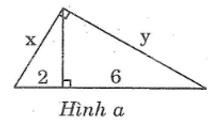
Hãy tính x và y trong các hình sau:
Lời giải:
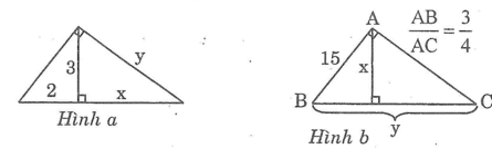
a. Hình a:
Theo định lí Pi-ta-go, ta có:
Theo hệ thức liên hệ giữ cạnh góc vuông và hình chiếu của nó, ta có:
b. Hình b:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
142 = y.16
x + y = 15 ⇒ x = 16 – y = 16 – 12,25 = 3,75
Bài 2 trang 102 Sách bài tập Toán 9 Tập 1:
Hãy tính x và y trong các hình sau:
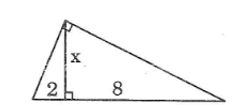
a. Hình a:
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
x2 = 2.(2 + 6) = 2.8 = 16 ⇒ x = 4
y2 = 6.(2 + 6) = 6.8 = 48 ⇒ y = √48 = 4√3
b. Hình b:
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
x2 = 2.8 = 16 ⇒ x = 4
Bài 3 trang 103 Sách bài tập Toán 9 Tập 1:
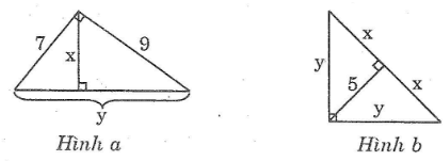
Hãy tính x và y trong các hình sau:
Lời giải:
a. Hình a:
Theo định lí Pi-ta-go, ta có:
y2 = 72 + 92 ⇒ y =
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
x.y = 7.9 ⇒ x =
b. Hình b:
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
52 = x.x = x2 ⇒ x = 5
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
y2 = x.(x + x) = 5.(5 + 5) = 50 ⇒ y = √50 = 5√2
Bài 4 trang 103 Sách bài tập Toán 9 Tập 1:
Hãy tính x và y trong các hình sau:
Lời giải:
a. Hình a:
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
32 = 2.x ⇒ x = 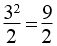
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
y2 = x.(x + 2) = 4,5.(4,5 + 2) = 29,25 ⇒ y = √29,25
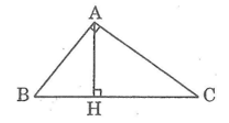
b. Hình b:
Ta có: 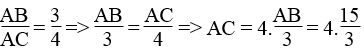
Theo định lí Pi-ta-go, ta có:
y2 = BC2 = AB2 + AC2 = 152 + 202 = 625
Suy ra: y = √625 = 25
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
x.y = 15.20 ⇒ x = 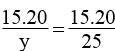
Bài 5 trang 103 Sách bài tập Toán 9 Tập 1:
Cho tam giác ABC vuông tại A, đường cao AH. Giải bài toán trong mỗi trường hợp sau:
a. Cho AH = 16, BH = 25. Tính AB, AC, BC, CH
b. Cho AB = 12, BH = 6. Tính AH, AC, BC, CH
Lời giải:
a. Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: AH2 = BH.CH
⇒ CH =
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC ⇒ AB =
≈ 29,68
AC2 = HC.BC
⇒ AC = 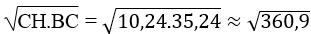
b. Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC ⇒ BC = 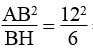
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
AC2 = HC.BC ⇒ AC = 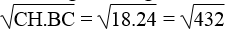
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
AH2 = HB.BC ⇒ AH =
Bài 6 trang 103 Sách bài tập Toán 9 Tập 1:
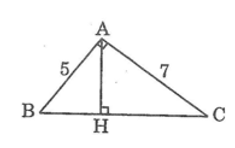
Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.
Lời giải:
Giả sử tam giác ABC có 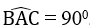
Theo định lí Pi-ta-go, ta có:
BC2 = AB2 + AC2
⇒ BC =
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
AH.BC = AB.AC ⇒ AH =
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
AB2 = BH.BC ⇒ BH =
CH = BC – BH =
Bài 7 trang 103 Sách bài tập Toán 9 Tập 1:
Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.
Lời giải:
Giả sử tam giác ABC có góc BAC = 90o, AH ⊥ BC, BH = 3, CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC = 3.(3 + 4) = 3.7 = 21 ⇒ AB = √21
AC2 = CH.BC = 4.(3 + 4) = 4.7 = 28 ⇒ AC = √28 = 2√7
Bài 8 trang 103 Sách bài tập Toán 9 Tập 1:
Cạnh huyển của một tam giác vuông lớn hơn một cạnh góc vuông là 1 cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyển là 4cm. Hãy tính các cạnh của tam giác vuông này.
Lời giải:
Giả sử tam giác ABC có góc (BAC) = 90o
Theo đề bài, ta có: BC – AB = 1 (cm) (1)
AB + AC – BC = 4 (cm) (2)
Từ (1) và (2) suy ra: BC – AB + AB + AC – BC = 4 + 1 = 5 (cm)
Theo định lí Pi-ta-go, ta có: BC2 = AB2 + AC2 (3)
Từ (1) suy ra: BC = AB + 1 (4)
Thay (4) vào (3) ta có:
(AB + 1)2 = AB2 + AC2
⇔ AB2 + 2AB + 1 = AB2 + 52
⇔ 2AB = 24 ⇔ AB = 12 (cm)
Thay AB = 12 (cm) vào (1) ta có: BC = 12 + 1 = 13 (cm)
Bài 9 trang 104 Sách bài tập Toán 9 Tập 1:
Một tam giác vuông có cạnh huyền là 5 và đường cao tương ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
Lời giải:
Giả sử tam giác ABC có góc (BAC) = 90o, AH ⊥ BC, BC = 5, AH = 2 và BH < CH
Ta có: BH + CH = 5 (1)
Theo hệ thức liên hệ giữa đường cao và cạnh huyền trong tam giác, ta có:
BH.CH = AH2 = 22 = 4 (2)
Từ (1) và (2) suy ra: BH = 1 và CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC = 1.5 = 5
Suy ra: AB = 5
Bài 10 trang 104 Sách bài tập Toán 9 Tập 1:
Cho một tam giác vuông. Biết tỉ số hai cạn góc vuông là 3 : 4 và cạnh huyền là 125 cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.