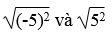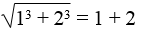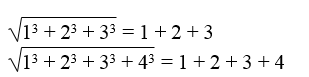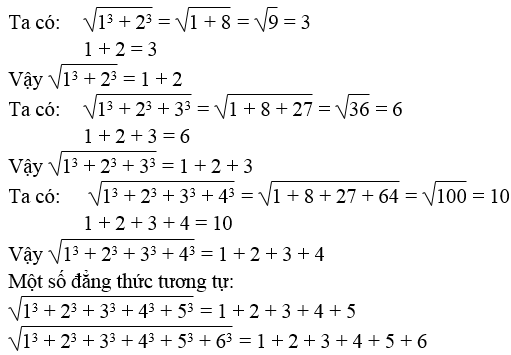Bài 1: Căn bậc hai
Bài 1 trang 5 Sách bài tập Toán 9 Tập 1:
Tính căn bậc hai số học của:
a. 0,01 b. 0,04 c. 0,49 d. 0,64
e. 0,25 f. 0,81 g. 0,09 h. 0,16
Lời giải:
a. √0,01 = 0,1 vì 0,1 ≥ 0 và (0,1)2 = 0,01
b. √0,04 = 0,2 vì 0,2 ≥ 0 và (0,2)2 = 0,04
c. √0,49 = 0,7 vì 0,7 ≥ 0 và (0,7)2 = 0,49
d. √0,64 = 0,8 vì 0,8 ≥ 0 và (0,8)2 = 0,64
e. √0,25 = 0,5 vì 0,5 ≥ 0 và (0,5)2 = 0,25
f. √0,81 = 0,9 vì 0,9 ≥ 0 và (0,9)2 = 0,81
g. √0,09 = 0,3 vì 0,3 ≥ 0 và (0,3)2 = 0,09
h. √0,16 = 0,4 vì 0,4 ≥ 0 và (0,4)2 = 0,16
Bài 2 trang 5 Sách bài tập Toán 9 Tập 1:
Dùng máy tính bỏ túi tim x thỏa mãn đẳng thức (làm tròn đến chữ số thập phân thứ ba).
a. x2 = 5 b. x2 = 6
c. x2 = 2,5 d. x2 = √5
Lời giải:
a. x2 = 5 ⇒ x1 = 5 và x2 = -5
Ta có: x1 = 5 ≈ 2,236 và x2 = – 5 = -2,236
b. x2 = 6 ⇒ x1 = 6 và x2 = – 6
Ta có: x1 = 6 ≈ 2,449 và x2 = – 6 = -2,449
c. x2 = 2,5 ⇒ x1 = √2,5 và x2 = – √2,5
Ta có: x1 = √2,5 ≈ 1,581 và x2 = – √2,5 = -1,581
d. x2 = 5 ⇒ x1 = √(√5) và x2 = √(√5)
Ta có: x1 = √(√5) ≈ 1,495 và x2 = – √(√5) = -1,495
Bài 3 trang 5 Sách bài tập Toán 9 Tập 1:
Số nào có căn bậc hai là:
a. √5 b. 1,5 c. -0,1 d. -√9
Lời giải:
a. Số 5 có căn bậc hai là √5
b. Số 2,25 có căn bậc hai là 1,5
c. Số 0,01 có căn bậc hai là -0,1
d. Số 9 có căn bậc hai là -√9
Bài 4 trang 5 Sách bài tập Toán 9 Tập 1:
Tìm x không âm biết:
a. √x = 3 b. √x = √5 c. √x = 0 d. √x = -2
Lời giải:
a. √x = 3 ⇒ x = 32 ⇒ x = 9
b. √x = √5 ⇒ x = (√5 )2 ⇒ x = 5
c. √x = 0 ⇒ x = 02 ⇒ x = 0
d. Căn bậc hai số học là số không âm nên không tồn tại giá trị nào của √x thỏa mãn x = -2
Bài 5 trang 6 Sách bài tập Toán 9 Tập 1:
So sánh (không dùng bảng số hay máy tính bỏ túi)
a. 2 và √2 + 1 b. 1 và √3 – 1
c. 2√31 và 10 d. -√3.11 và -12
Lời giải:
a. Ta có: 1 < 2 ⇒ √1 < √2 ⇒ 1 < √2
Suy ra: 1 + 1 < √2 + 1
Vậy 2 < √2 + 1
b. Ta có: 4 > 3 ⇒ √4 > √3 ⇒ 2 > √3
Suy ra: 2 – 1 > √3 – 1
Vậy 1 > √3 – 1
c. Ta có: 31 > 25 ⇒ √31 > √25 ⇒ √31 > 5
Suy ra: 2.√31 > 2.5
Vậy 2.√31 > 10
d. Ta có: 11 < 16 ⇒ √11 < √16 ⇒ √11 < 4
Suy ra: -3.√11 > -3.4
Vậy -3√11 > -12
Bài 6 trang 6 Sách bài tập Toán 9 Tập 1:
Tìm những khẳng định đúng trong các khẳng định sau:
a. Căn bậc hai của 0,36 là 0,6
b. Căn bậc hai của 0,36 là 0,06
c. √0,36 = 0,6
d. Căn bậc hai của 0,36 là 0,6 và -0,6
e. √0,36 = ± 0,6
Lời giải:
Câu a và c đúng.
Bài 7 trang 6 Sách bài tập Toán 9 Tập 1:
Trong các số 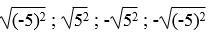
Lời giải:
Căn bậc hai số học của 25 là
Bài 8 trang 6 Sách bài tập Toán 9 Tập 1:
Chứng minh:
Viết tiếp một số đẳng thức tương tự.
Lời giải:
Bài 9 trang 6 Sách bài tập Toán 9 Tập 1:
Cho hai số a, b không âm. Chứng minh:
a. Nếu √a < √b thì a < b
b. Nếu a < b thì √a < √b
Lời giải:
a. a ≥ 0; b ≥ 0 và a < b ⇒ b > 0
Ta có: √a ≥ 0; √b ≥ 0 suy ra: √a + √b > 0 (1)
Mặt khác: a – b = (√a )2 – (√b )2 = (√a + √b )(√a – √b )
Vì a < b nên a – b < 0
Suy ra: (√a + √b )(√a – √b ) < 0 (2)
Từ (1) và (2) suy ra: √a – √b < 0 ⇒ √a < √b
b. a ≥ 0; b ≥ 0 và √a < √b ⇒ √b > 0
Suy ra: √a + √b > 0 và √a – √b < 0
(√a + √b )(√a – √b ) < 0
⇒ (√a )2 – (√b )2 < 0 ⇒ a – b < 0 ⇒ a < b
Bài 10 trang 6 Sách bài tập Toán 9 Tập 1:
Cho số m dương. Chứng minh:
a. Nếu m > 1 thì √m > 1 b. Nếu m < 1 thì √m < 1
Lời giải:
a. Ta có: m > 1 ⇒ √m > √1 ⇒ √m > 1
b. Ta có: m < 1 ⇒ √m < √1 ⇒ √m < 1
Bài 11 trang 6 Sách bài tập Toán 9 Tập 1: Cho số m dương. Chứng minh:
a. Nếu m > 1 thì m > √m b. Nếu m < 1 thì m < √m
Lời giải:
a. Ta có: m > 1 ⇒ √m > √1 ⇒ √m > 1
Vì m > 0 nên √m > 0
Suy ra: √m .√m > 1.√m ⇒ m > √m
b. Ta có: m < 1 ⇒ √m < √1 ⇒ √m < 1
Vì m > 0 nên √m > 0
Suy ra: √m .√m < 1.√m ⇒ m < √m
Bài 1 trang 7 Sách bài tập Toán 9 Tập 1:
Lời giải:
≠ khác ∈ thuộc ⇔ tương đương
√ căn bậc hai ≈ xấp xỉ 2
<, >, ≥, ≤ Δ tam giác ∠góc, ⊥ vuông góc ⇒ suy ra, ABCD.A1B1C1D1 X−