GIẢI BÀI TẬP XÁC SUẤT CỦA BIẾN CỐ
- “Giải bài tập xác suất của biến cố” gồm có 3 phần lớn: Phần A – Tóm tắt lý thuyết, Phần B – Các dạng bài tập và phương phải giải bài tập xác suất của biến cố, Phần C – Giải các bài tập xác suất của biến cố.
- Phần A – Tóm tắt lại các định nghĩa, tính chất, quy tắc của xác suất.
- Phần B – Gồm có 3 dạng bài tập xác suất của biến cố và phương pháp giải bài tập xác suất của biến cố.
- Phần C – Giải bài tập xác suất của biến cố.
PHỤ HUYNH VÀ HỌC SINH CÓ THỂ TÌM HIỂU THÊM
Xác suất: Lý thuyết và bài tập
Các bài tập xác suất khó trong luyện thi đại học
A. Tóm tắt lý thuyết:
- Xác suất của biến cố:

- 0 ≤ P(A) ≤ 1
- P(Ω) = 1 ; P(∅)= 0
- Qui tắc cộng:
+) Nếu A ∩ B = ∅ thì P(A∪B) = P(A) + P(B)
+) Nếu A, B bất kì thì P(A∪B) = P(A) + P(B) – P(A.B)
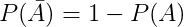
- Qui tắc nhân: Nếu A, B độc lập thì P(A.B)= P(A).P(B)
B. Các dạng bài tập và giải xác suất của biến cố:
I. DẠNG 1: XÁC ĐỊNH PHÉP THỬ, KHÔNG GIAN MẪU VÀ BIẾN CỐ
Phương pháp: Để xác định không gian mẫu và biến cố ta thường sử dụng các cách sau
Cách 1: Liệt kê các phần tử của không gian mẫu và biến cố rồi chúng ta đếm.
Cách 2:Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố.
II. DẠNG 2: TÌM XÁC SUẤT CỦA BIẾN CỐ
Phương pháp:
Tính xác suất theo thống kê ta sử dụng công thức: 
Tính xác suất của biến cố theo định nghĩa cổ điển ta sử dụng công thức: 
III. DẠNG 3: CÁC QUY TẮC TÍNH XÁC SUẤT
Bài toán 01: Tính xác suất bằng quy tắc cộng
Phương pháp: Sử dụng các quy tắc đếm và công thức biến cố đối, công thức biến cố hợp.
P(A∪B) = P(A) + P(B) với 2 biến cố A, B xung khắc.
![]()
Bài toán 02: Tính xác suất bằng quy tắc nhân
Phương pháp:
Để áp dụng quy tắc nhân ta cần:
Chứng tỏ A và B độc lập
Áp dụng công thức: P(A.B)= P(A).P(B)
C. Giải bài tập xác suất của biến cố:
I. Dạng 1:









II. Dạng 2:




III. Dạng 3:



