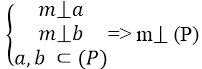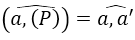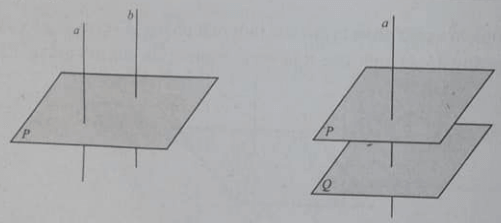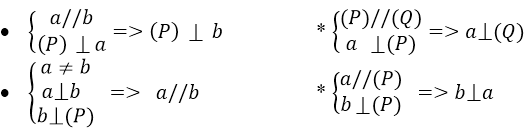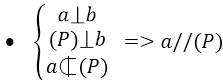Lý thuyết: Đường thẳng vuông góc với mặt phẳng
1. Về kiến thức.
– Định nghĩa: đường thẳng vuông góc với mặt phẳng khi nó vuông góc với mọi đường thẳng thuộc mặt phẳng đó.
Biết điều kiện để đường thẳng vuông góc với mặt phẳng: đường thẳng vuông góc với hai đường thẳng giao nhau thuộc mặt phẳng đó:
Hệ quả 1. Qua một điểm có một và chỉ một mặt phẳng vuông góc với một đường thẳng cho trước.
Hệ quả 2. Qua một điểm có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho trước.
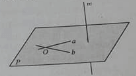
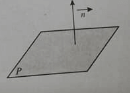
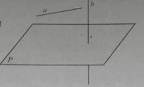
– Biết khái niệm vecto pháp tuyến của một mặt phẳng là vecto có giá vuông góc với mặt phẳng đó. ở hình sau, n→ là vecto pháp tuyến của mặt phẳng (P).
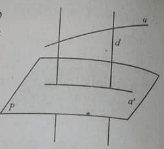
– Biết khái niệm phép chiếu vuông góc. Phép chiếu lên mặt phẳng (P) theo phương d vuông góc với (P) gọi là phép chiếu vuông góc.
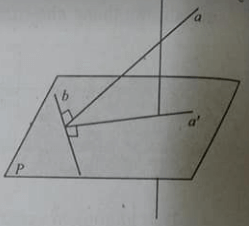
Hiểu khái niệm góc giữa đường thẳng a và mặt (P) là góc giữa a và hình chiếu a’ của a trên (P):
Nếu a vuông góc với (P) thì
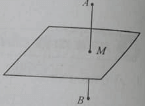
– Biết khái niệm mặt phẳng trung trực của đoạn thẳng là mặt phẳng đi qua trung điểm và vuông góc với đoạn thẳng đó
Lưu ý: mặt phẳng trung trực (P) của đoạn thẳng AB là tập hợp các điểm cách đều hai đầu A và B.
2. Về kĩ năng.
– Cách chứng minh đường thẳng vuông góc với mặt phẳng: đường thẳng đó vuông góc với hai đường thẳng giao nhau thuộc mặt phẳng.
– Cách chứng minh đường thẳng vuông góc với đường thẳng. góc giữa hai đường thẳng đó bằng 900; tích vô hướng của hai vecto chỉ phương của hai đường thẳng đó bằng 0; một đường thẳng vuông góc với mặt phẳng có chứa đường thẳng kia.
– Xác định được vecto pháp tuyến của một mặt phẳng; hình chiếu vuông góc của một điểm, một đường thẳng và một tam giác ; góc giữa đường thẳng và mặt phẳng.
– Vận dụng được định lí ba đường vuông góc. Cho đường thẳng a có hình chiếu lên mặt phẳng (P) là a’, b ⊥ a ⇒ b ⊥ a’.
– Xác định mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.