Lý thuyết về dấu của tam thức bậc 2
Sẽ giúp các em học sinh biết khi nào tam thức luôn âm, luôn dương, trong trái ngoài cùng….
Xem thêm về lý thuyết tam thức bậc hai, tam thức bậc 2
Định lí Viet thuận và đảo trong phương trình bậc hai -tam thức bậc hai
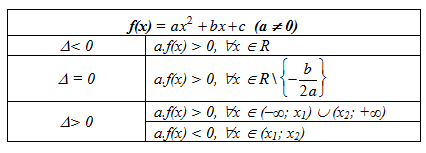
1. Định nghĩa tam thức bậc hai
Tam thức bậc hai là biểu thức có dạng f(x)=ax2+bx+c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
– Định lí thuận về dấu của tam thức bậc 2:
Cho tam thức bậc hai f(x)=ax2+bx+c (a ≠ 0)
có biệt thức Δ=b2−4ac
– Nếu ∆ < 0 thì a.f(x) > 0 với ∀ x ∈ R
– Nếu ∆ = 0 thì a.f(x) > 0 với ∀ x # −b2a hoặc a.f(x) ≥ 0 với ∀ x ∈ R
– Nếu ∆ > 0 thì ⎧⎩⎨⎪⎪a.f(x)>0⇔[x<x1x>x2a.f(x)<0⇔x1<x<x2
– Định lí đảo về dấu của tam thức bậc 2:
Cho tam thức bậc hai f(x)=ax2+bx+c (a ≠ 0)
Nếu có số α thỏa mãn a.f(α) < 0 thì f(x) có 2 nghiệm phân biệt x1,x2 và x1<x<x2
+ Hệ quả:
a.f(α) < 0 ⇔ {Δ>0x1<a<x2
{Δ>0a.f(α)>0 ⇔ α ∉ [latex]\displaystyle {{x}_{1}};{{x}_{2}}[/latex]
a.f(α) = 0 ⇔ α là nghiệm của f(x)
2. Khái niệm bất phương trình bậc hai một ẩn
Bất phương trình bậc hai một ẩn là mệnh đề chứa một biến có một trong các dạng:
ax2+bx+c > 0, ax2+bx+c < 0, ax2+bx+c ≥ 0, ax2+bx+c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn trên ta dùng định lí thuận về dấu của tam thức bậc hai.