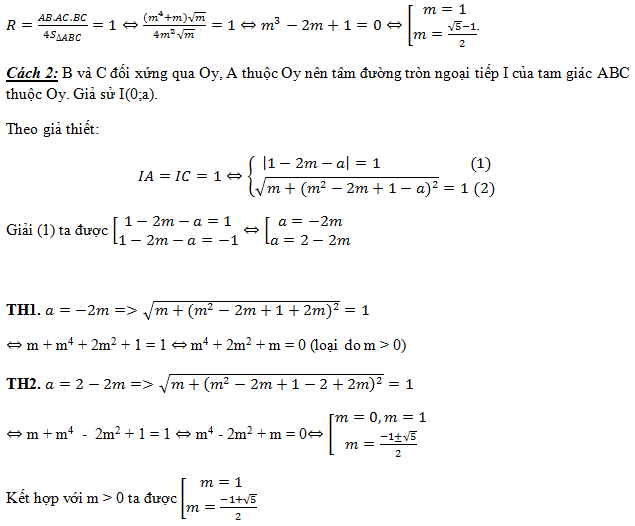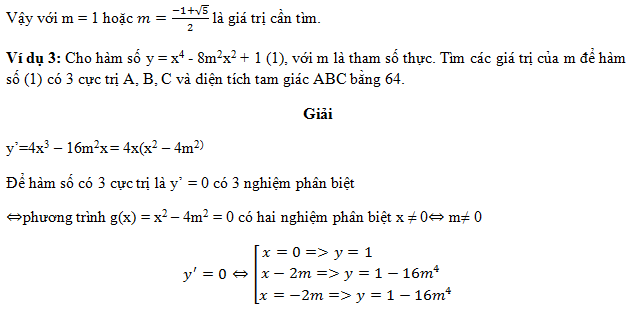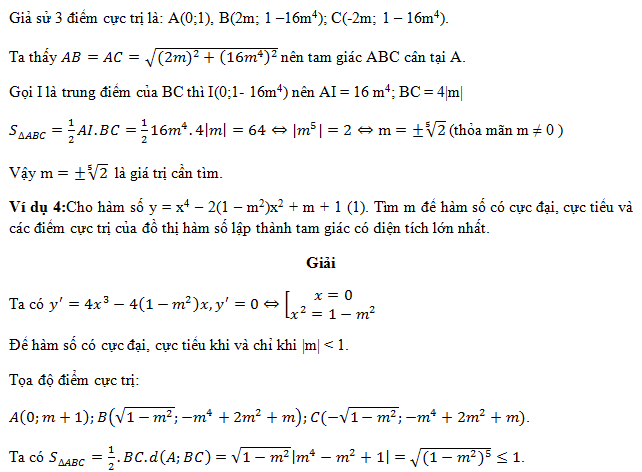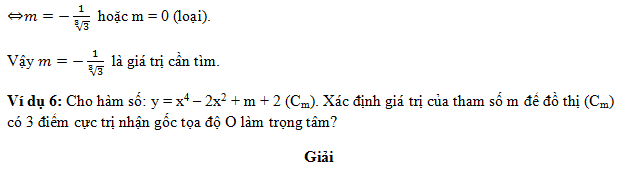Bài toán tổng quát: Cho hàm số y = ax4 + bx2 + c (a, b, c phụ thuộc vào tham số m). Tìm m để hàm số có 3 cực trị và thỏa mãn điều kiện cho trước.
Phương pháp:
Bước 1: Đạo hàm y’ = 4ax3 + 2bx = 2x(2ax2 + b) = 2x.g(x) với g(x) = 2ax2 + b
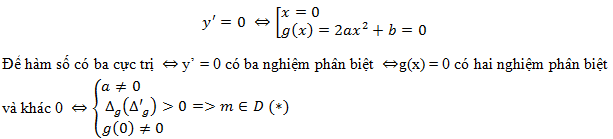
Nhận xét: Phương trình y’ = 0 luôn có một nghiệm x = 0 và đồ thị hàm ban đầu là hàm số chẵn nên các điểm cực trị đối xứng nhau qua Oy.
Giả sử ba điểm cực trị là A ∈ Oy, B và C đối xứng nhau qua Oy.
Bước 2: Từ điều kiện cho trước dẫn tới một phương trình (hoặc bất phương trình) theo tham số. Giải phương trình này ta được giá trị của tham số, đối chiếu với điều kiện (*) và kết luận.
VÍ DỤ MINH HỌA
Ví dụ 1: Cho hàm số y = x4 – 2(m+1)x2 + m2 (1), với m là tham số thực. Tìm m để đồ thị hàm số (1) có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông.
Giải
Đạo hàm y’ = 4x3 – 4(m + 1)x.
![]()
Hàm số có 3 cực trị m + 1 > 0 ⇔ m > -1
Khi đó đồ thị hàm số có 3 cực trị:
![]()
Nhận xét: A ∈ Oy, B và C đối xứng nhau qua Oy nên ∆ABC cân tại A tức là AB = AC nên tam giác chỉ có thể vuông cân tại A.
Cách 1: Gọi M là trung điểm của BC=>M(0; -2m – 1)
Do đó để tam giác ABC vuông cân ⇔ BC = 2AM (đường trung tuyến bằng nửa cạnh huyền)
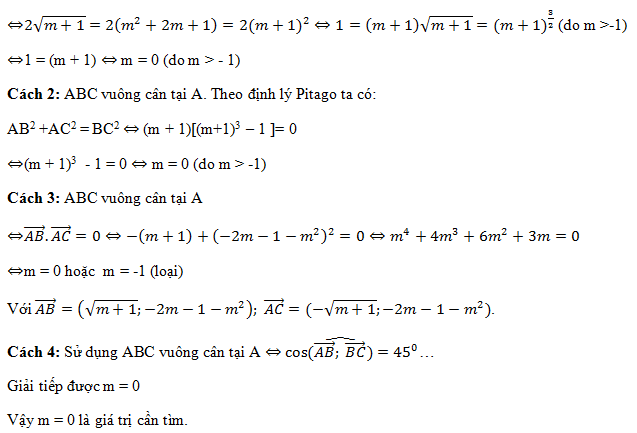
Ví dụ 2: Cho hàm số y = x4 – 2mx2 + m -1 (1), với m là tham số thực. Xác định các giá trị của tham số m để hàm số (1) có ba cực trị, đồng thời các giá trị của hàm số tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Giải