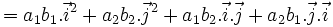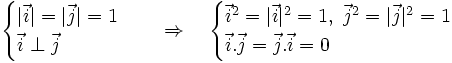Bài viết sau đây sẽ giới thiệu cho các em về những công thức quan trọng về tích vô hướng của hai vectơ:
Tìm hiểu thêm về tích vô hướng tại đây:
- Tích vô hướng : Lý thuyết và bài tập
- Tích vô hướng của hai vectơ – lớp 10
- Tính tích vô hướng hai vectơ bằng máy tính Casio
Góc giữa hai vectơ
Cho hai vectơ  và
và  đều khác vectơ
đều khác vectơ  .
.
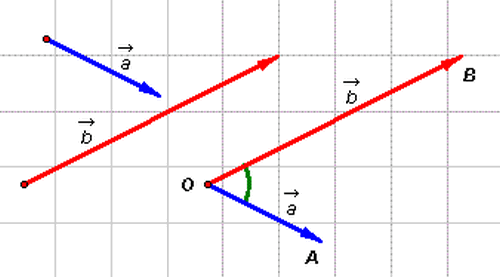
Từ một điểm O bất kì, ta vẽ các vectơ 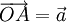 và
và  (hình 2-6). Khi đó:
(hình 2-6). Khi đó:
|
Số đo của góc AOB được gọi là số đo của góc giữa hai vectơ
 và và  , hoặc đơn giản là góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ  và và  . . |
|
CHÚ Ý:
- Góc giữa hai vectơ
 và
và  được kí hiệu là
được kí hiệu là 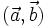 .
. - Từ định nghĩa ta có
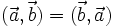
- Nếu
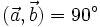 thì ta nói rằng hai vectơ
thì ta nói rằng hai vectơ  và
và  vuông góc với nhau, kí hiệu là
vuông góc với nhau, kí hiệu là 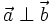 .
. - Trong trường hợp có ít nhất một trong hai vectơ là vectơ-không thì ta xem góc giữa hai vectơ đó là tùy ý (từ 0° đến 180°).
- Số đo của góc AOB là không đổi, dù ta có chọn điểm O ở các vị trí khác nhau. Do đó, khi xác định góc giữa hai vectơ
 và
và  ta thường chọn điểm Otrùng với điểm gốc của vectơ
ta thường chọn điểm Otrùng với điểm gốc của vectơ  hoặc vectơ
hoặc vectơ  . Và theo định nghĩa ta có:
. Và theo định nghĩa ta có:
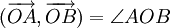 |
Tích vô hướng của hai vectơ[sửa]
Trong Vật lí, ta có khái niệm “công sinh bởi một lực“.
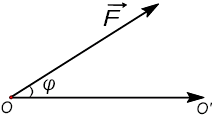
Giả sử một lực không đổi 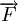 tác dụng lên một vật làm cho nó di chuyển từ điểm O đến O’ (hình vẽ).
tác dụng lên một vật làm cho nó di chuyển từ điểm O đến O’ (hình vẽ).
Khi đó lực 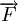 đã sinh ra một công A tính theo công thức:
đã sinh ra một công A tính theo công thức:
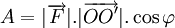 trong đó:
trong đó:
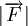 là cường độ của lực
là cường độ của lực 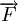 tính bằng Niutơn (kí hiệu là N);
tính bằng Niutơn (kí hiệu là N);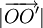 là độ dài vectơ
là độ dài vectơ 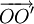 tính bằng mét (kí hiệu là m);
tính bằng mét (kí hiệu là m);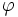 là góc giữa hai vectơ
là góc giữa hai vectơ 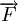 và
và 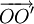 .
.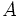 là công do lực
là công do lực 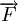 sinh ra, được tính bằng Jun (kí hiệu là J).
sinh ra, được tính bằng Jun (kí hiệu là J).
Trong Toán học, giá trị của biểu thức 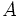 (không kể đơn vị đo) được gọi là tích vô hướng của hai vectơ
(không kể đơn vị đo) được gọi là tích vô hướng của hai vectơ 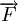 và
và 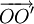 . Tổng quát, ta có định nghĩa sau về tích vô hướng của hai vectơ bất kì
. Tổng quát, ta có định nghĩa sau về tích vô hướng của hai vectơ bất kì  và
và  .
.
|
Tích vô hướng của hai vectơ
 và và  là một số, kí hiệu là là một số, kí hiệu là 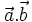 , được xác định bởi công thức: , được xác định bởi công thức: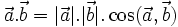 (1) (1) |
Bình phương vô hướng
Khi 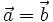 thì công thức (1) trở thành:
thì công thức (1) trở thành:
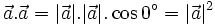
Người ta kí hiệu tích vô hướng 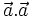 là
là 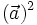 hay đơn giản hơn là
hay đơn giản hơn là 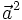 và gọi là bình phương vô hướng của vectơ
và gọi là bình phương vô hướng của vectơ  .
.
Như vậy, ta có:
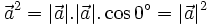
Tính chất của tích vô hướng
Với hai số thực a và b, ta có ab = ba; a(b + c) = ab + ac. Vậy với hai vectơ  và
và  , ta có các tính chất tương tự hay không?
, ta có các tính chất tương tự hay không?
|
Với ba vectơ
|
Ta dễ dàng chứng minh được các tính chất 1, 2. Tính chất 3 được thừa nhận không chứng minh.
Dùng các tính chất của tích vô hướng, ta chứng minh được các hệ thức sau:
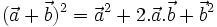 |
(1) |
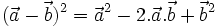 |
(2) |
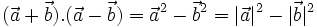 |
(3) |
Chẳng hạn, hệ thức (3) được chứng minh như sau. Theo tính chất phân phối, ta có:
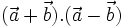 |
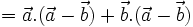 |
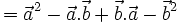 |
|
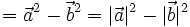 |
Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng toạ độ 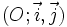 , cho hai vectơ
, cho hai vectơ 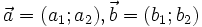 .
.
Khi đó, ta có công thức:
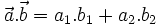 |
Thật vậy:
NHẬN XÉT
Hai vectơ 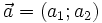 và
và 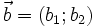 khác vectơ
khác vectơ  vuông góc với nhau khi và chỉ khi
vuông góc với nhau khi và chỉ khi 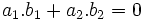
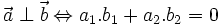 |
Độ dài của vectơ
Độ dài của vectơ 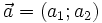 được tính theo công thức:
được tính theo công thức:
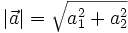 |
Thật vậy, ta có: 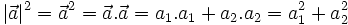
Do đó 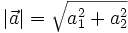 (đpcm).
(đpcm).
Góc giữa hai vectơ
Với hai vectơ 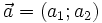 và
và 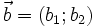 khác vectơ
khác vectơ  , từ định nghĩa của tích vô hướng và hệ thức độ dài trên, ta suy ra góc giữa hai vectơ được xác định bởi hệ thức sau:
, từ định nghĩa của tích vô hướng và hệ thức độ dài trên, ta suy ra góc giữa hai vectơ được xác định bởi hệ thức sau:
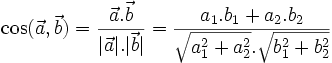 |
Khoảng cách giữa hai điểm 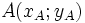 và
và 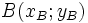 được tính theo công thức sau:
được tính theo công thức sau:
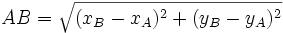 |
Thật vậy
- Vì
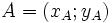 và
và 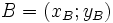 nên
nên 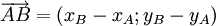
- Từ (1) suy ra
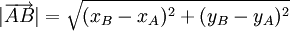
- Mặt khác
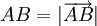 , kết hợp với (2) ta có
, kết hợp với (2) ta có 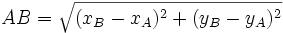 (đpcm)
(đpcm)
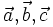 tùy ý và mọi số thực k, ta có:
tùy ý và mọi số thực k, ta có: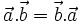 (
(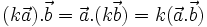
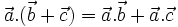 (
(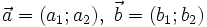
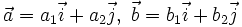 .
.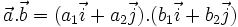 .
.