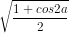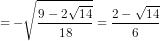Công thức lượng giác Toán lớp 10

March 11, 2016

Công thức lượng giác Toán lớp 10

Công thức lượng giác cần nhớ

[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]

Bài 1 trang 153 sgk đại số 10

a) cos225⁰ , sin240⁰ , cot(-15⁰ ), tan 75⁰ ;

b) sin $\frac{7x}{12}$ , cos $\left ( -\frac{\prod }{12} \right )$ , tan $\left ( \frac{13\prod }{12} \right )$

Hướng dẫn giải:

a) + cos225⁰ = cos(180⁰ + 45⁰ ) = -cos45⁰= $-\frac{\sqrt{2}}{2}$

+ sin240⁰ = sin(180⁰ + 60⁰ ) = -sin60⁰ = $-\frac{\sqrt{3}}{2}$

+ cot(-15⁰ ) = -cot15⁰ = -tan75⁰ = -tan(30⁰ + 45⁰ )

$=\frac{-tan30^{0}-tan45^{0}}{1-tan30^{0}tan45^{0}}=\frac{-\frac{1}{\sqrt{3}}-1}{1-\frac{1}{\sqrt{3}}}=-\frac{\sqrt{3}+1}{\sqrt{3}-1}=-\frac{(\sqrt{3}+1)^{2}}{2}$

= -2 – √3

+ tan 75⁰ = cot15⁰= 2 + √3

+ sin $\frac{7x}{12}$ = sin $\left ( \frac{\coprod }{3}+\frac{\coprod }{4} \right )$ = sin $\frac{\coprod }{3}$ cos $\frac{\coprod }{4}$ + cos $\frac{\coprod }{3}$ sin $\frac{\coprod }{4}$

$=\frac{\sqrt{2}}{2}\left ( \frac{\sqrt{3}}{2} +\frac{1}{2}\right )=\frac{\sqrt{6}+\sqrt{2}}{4}$

+ cos $\left ( -\frac{\prod }{12} \right )$ = cos $\left ( \frac{\prod }{4} -\frac{\prod }{3}\right )$ = cos $\frac{\prod }{4}$ cos $\frac{\prod }{3}$ + sin $\frac{\prod }{3}$ sin $\frac{\prod }{4}$

$=\frac{\sqrt{2}}{2}\left ( \frac{\sqrt{3}}{2} +\frac{1}{2}\right )=0,9659$ $\frac{\sqrt{2}}{2}\left ( \frac{\sqrt{3}}{2} +\frac{1}{2}\right )=0,9659$

+ tan $\left ( \frac{13\prod }{12} \right )$ = tan(π + $\frac{\prod }{12}$ ) = tan $\frac{\prod }{12}$ = tan $\left ( \frac{\coprod }{3}-\frac{\coprod }{4} \right )$ = $\frac{tan\frac{\prod }{3}-tan\frac{\prod }{4}}{1+tan\frac{\prod }{3}tan\frac{\prod }{4}}=\frac{\sqrt{3}-1}{1+\sqrt{3}}$

= 2 – √3

Bài 2 trang 154 sgk đại số 10

Bài 2. Tính

a) cos(α + $\frac{\prod }{3}$ ), biết sinα = $\frac{1}{\sqrt{3}}$ và 0 < α < $\frac{\prod }{2}$ .

b) tan(α – $\frac{\prod }{4}$ ), biết cosα = – $\frac{1}{3}$ và $\frac{\prod }{2}$ < α < π

c) cos(a + b), sin(a – b),

biết sina = $\frac{4}{5}$ , 0⁰ < a < 90⁰ và sin b = $\frac{2}{3}$ , 90⁰ < b < 180⁰

Hướng dẫn giải:

a) Do 0 < α < $\frac{\prod }{2}$ nên sinα > 0, cosα > 0

cosα = $\sqrt{1-sin^{2}\alpha }=\sqrt{1-\frac{1}{3}}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}$

cos(α + $\frac{\prod }{3}$ ) = cosαcos $\frac{\prod }{3}$ – sinαsin $\frac{\prod }{3}$

= $\frac{\sqrt{6}}{3}.\frac{1}{2}-\frac{1}{\sqrt{3}}.\frac{\sqrt{3}}{2}=\frac{\sqrt{6}-3}{6}$

b) Do $\frac{\prod }{2}$ < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0

tanα = $-\sqrt{\frac{1}{cos^{2}\alpha }-1}=-\sqrt{3^{3}-1}$ = -2√2

tan(α – $\frac{\prod }{4}$ ) = $\frac{tan\alpha -tan\frac{\prod }{4}}{1+tan\alpha tan\frac{\prod }{4}}=\frac{-1-2\sqrt{2}}{1-2\sqrt{2}}=\frac{2\sqrt{2}+1}{2\sqrt{2}-1}$

c) 0⁰ < a < 90⁰ => sina > 0, cosa > 0

90⁰ < b < 180⁰ => sinb > 0, cosb < 0

cosa = $\sqrt{1-sin^{2}a}=\sqrt{1-\left ( \frac{4}{5} \right )^{2}}=\frac{3}{5}$

cosb = $-\sqrt{1-sin^{2}a}=-\sqrt{1-\left ( \frac{2}{3} \right )^{2}}=-\frac{\sqrt{5}}{3}$

cos(a + b) = cosacosb – sinasinb

$=\frac{3}{5}\left ( -\frac{\sqrt{5}}{3} \right )-\frac{4}{5}.\frac{2}{3}=-\frac{3\sqrt{5}+8}{15}$

Bài 3 trang 154 sgk đại số 10

Bài 3. Rút gọn các biểu thức

a) sin(a + b) + sin( $\frac{\prod }{2}$ – a)sin(-b).

b) cos( $\frac{\prod }{4}$ + a)cos( $\frac{\prod }{4}$ – a) + $\frac{1 }{2}$ sin²a

c) cos( $\frac{\prod }{2}$ – a)sin( $\frac{\prod }{2}$ – b) – sin(a – b)

Hướng dẫn giải:

a) sin(a + b) + sin( $\frac{\prod }{2}$ – a)sin(-b) = sinacosb + cosasinb – cosasinb = sinacosb

b) cos( $\frac{\prod }{4}$ + a)cos( $\frac{\prod }{4}$ – a) + $\frac{1 }{2}$ sin²a

$=\frac{1 }{2}cos\left [ \frac{\prod }{4}+a+\frac{\prod }{4} -a\right ]+\frac{1}{2}cos\left [ \left ( \frac{\prod }{4} +a\right ) -\left ( \frac{\prod }{4}-a \right )\right ]+\frac{1}{2}\left ( \frac{1-cos2a}{2} \right )$

$=\frac{1}{2}$ cos2a + $\frac{1}{4}$ (1 – cos2a) = $\frac{1+cos2a}{4 }=$ $\frac{1 }{2}$ cos²a

c) cos( $\frac{\prod }{2}$ – a)sin( $\frac{\prod }{2}$ – b) – sin(a – b) = sinacosb – sinacosb + sinbcosa

= sinbcosa

Bài 4 trang 154 sgk đại số 10

Bài 4. Chứng minh các đẳng thức

a) $\frac{cos(a-b)}{cos(a+b)}=\frac{cotacotb+1}{cotacotb-1}$

b) sin(a + b)sin(a – b) = sin²a – sin²b = cos²b – cos²a

c) cos(a + b)cos(a – b) = cos²a – sin²b = cos²b – sin²a

Hướng dẫn giải:

a) VT = $\frac{cosacosb+sinasinb}{cosacosb-sinasinb}=\frac{\frac{cosacosb}{sinasinb}+1}{\frac{cosacosb}{sinasinb}-1}=\frac{cotacotb+1}{cotacotb-1}$

b) VT = [sinacosb + cosasinb][sinacosb – cosasina]

= (sinacosb)² – (cosasinb)² = sin² a(1 – sin² b) – (1 – sin² a)sin² b

= sin²a – sin²b = cos²b( 1– cos²a) – cos² a(1 – cos² b) = cos²b – cos²a

c) VT = (cosacosb – sinasinb)(cosacosb + sinasinb)

= (cosacosb)² – (sinasinb)²

= cos² a(1 – sin² b) – (1 – cos² a)sin² b = cos² a – sin² b

= cos² b(1 – sin² a) – (1 – cos² b)sin² a = cos² b – sin² a

Bài 5 trang 154 sgk đại số 10

Bài 5. Tính sin2a, cos2a, tan2a, biết:

a) sina = -0,6 và π < a < $\frac{3\prod }{2}$ ;

b) cosa = – $\frac{5}{13}$ và $\frac{\prod }{2}$ < a < π

c) sina + cosa = $\frac{1 }{2}$ và $\frac{3\prod }{4}$ < a < π

Hướng dẫn giải:

a) π < a < $\frac{3\prod }{2}$ => sina < 0, cosa < 0, tana > 0

sin2a = 2sinacosa = 2(-0,6)(- $\sqrt{1-(0,6)^{2}}$ ) = 0,96

cos2a = cos² a – sin² a = 1 – 2sin² a = 1 – 0,72 = 0,28

tan2a = $\frac{0,96}{0,28}$ ≈ 3,1286

b) $\frac{\prod }{2}$ < a < π => sina > 0, cosa < 0

sina = $\sqrt{1-\left ( \frac{5}{13} \right )^{2}}=\frac{12}{13}$

sin2a = 2sinacosa = 2. $\frac{12}{13}\left ( -\frac{5}{13} \right )=-\frac{120}{169}$

cos2a = 2cos²a – 1 = 2 $\left ( \frac{5}{13} \right )^{2}$ – 1 = – $\frac{119}{169}$

tan2a = $\frac{sin2a}{cos2a}=\frac{120}{119}$

c) $\frac{3\prod }{4}$ < a < π => $\frac{3\prod }{2}$ < 2a < 2π => sin2a < 0, cos2a > 0, tan2a < 0

sin2a = $\frac{1}{4}$ – 1 = -0,75

cos2a = $\sqrt{1-\left ( \frac{3}{4} \right )^{2}}=\frac{\sqrt{7}}{4}$

tan2a = – $\frac{3}{\sqrt{7}}$

Bài 6 trang 154 sgk đại số 10

Bài 6. Cho sin 2a = – và < a < π.

Tính sina và cosa.

Hướng dẫn giải:

< a < π => sina > 0, cosa < 0

cos2a = = ±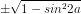

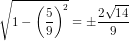
Nếu cos2a = 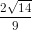thì

sina =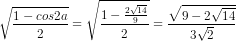

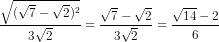
cosa = –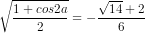

Nếu cos2a = –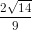 thì

sina =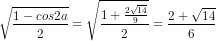

cosa = –

Công thức lượng giác, Toán

| Tags: Công thức lượng giácitconsultant

Thầy Nguyễn Thế Anh

Call Us: 0986683218