CHỈNH HỢP, TỔ HỢP

• “Chỉnh hợp, tổ hợp” gồm có 2 phần lớn: Phần A – Lý thuyết cơ bản, Phần B – Chú ý: Phân biệt chỉnh hợp, tổ hợp.
• Phần A gồm có 2 phần: Phần I – Chỉnh hợp (Lặp và không lặp), Phần II – Tổ hợp (Lặp và không lặp).

PHỤ HUYNH VÀ HỌC SINH CÓ THỂ TÌM HIỂU THÊM

Tổ hợp xác suất – Những điều cần biết

Chuyên đề tổ hợp xác suất

Bài tập tổ hợp xác suất khó

A. Lý thuyết cơ bản:

I. Chỉnh hợp:

1. Chỉnh hợp lặp:

• Định nghĩa:  Cho tập A gồm n phần tử. Mỗi dãy gồm k phần tử của A, trong đó mỗi phần tử có thể được lặp lại nhiều lần, được sắp xếp theo 1 thứ tự nhất định được gọi là một chỉnh hợp lặp chập k của n phần tử của tập A.
• Công thức:

– Số chỉnh hợp lặp chập k của n phần tử :      

2. Chỉnh hợp không lặp:

• Định nghĩa: Cho tập hợp A gồm n phần tử. Mỗi cách sắp xếp k phần tử của A (1≤k≤n) theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử của tập A.
• Công thức:

– Số chỉnh hợp chập k của n phần tử:

-Công thức trên cũng đúng trong trường hợp k = 0 hoặc k = n

– Khi k = n thì Aⁿ_n = P_n = n!

II. Tổ hợp:

1. Tổ hợp lặp:

• Định nghĩa: Cho tập A = {a₁,a₂,…,a_n}  và số tự nhiên k bất kỳ. Một tổ hợp lặp chập k của n phần tử là một tổ hợp gồm k phần tử, trong đó mỗi phần tử là một trong n phần tử của A.
• Công thức:

Số tổ hợp lặp chập k của n phần tử:           

2. Tổ hợp không lặp:

• Định nghĩa: Cho tập A gồm n phần tử. Mỗi tập con gồm k (1≤k≤n) phần tử của A được gọi là một tổ hợp chập k của n phần tử.
• Công thức:

– Số các tổ hợp chập k của n phần tử: 

• Tính chất: 

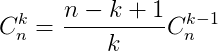
B. Chú ý: Phân biệt chỉnh hợp, tổ hợp:

• Chỉnh hợp, tổ hợp liên hệ nhau bởi công thức: 
• Chỉnh hợp, tổ hợp khác nhau:

– Chỉnh hợp có thứ tự.

– Tổ hợp không có thứ tự.

⇒ Những bài toán mà kết quả phụ thuộc vào các vị trí của các phần tử thì ta sẽ dùng chỉnh hợp. Ngược lại là tổ hợp.

• Cách lấy k phần tử từ tập n phần tử:

– Không có thứ tự, không hoàn lại: 

– Có thứ tự, không hoàn lại: 

– Có thứ tự, có hoàn lại: