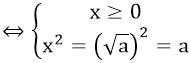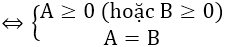Căn bậc hai: lý thuyết và bài tập

A. Lý thuyết:

I. Khái niệm căn bậc hai:

1. Định nghĩa: căn bậc hai của một số a là một số x sao cho x² = a, hay nói cách khác là số x mà bình phương lên thì = a.

2. Ví dụ: 3 và -3 là căn bậc hai của 9 vì 3² = (−3)² = 9.

Xem thêm: 

1. căn bậc hai: lý thuyết và bài tập
2. căn bậc hai lớp 9: cơ bản và nâng cao
3. căn bậc hai và hằng đẳng thức
4. bảng căn bậc hai
5. căn bậc hai số học
6. chuyên đề căn bậc hai toán 9
7. căn bậc 2 lớp 9 học gì?

II. Tính chất:

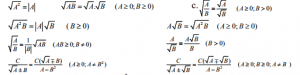
B. Bài tập:

Bài 1: Tính

a) Làm mất một lớp căn:

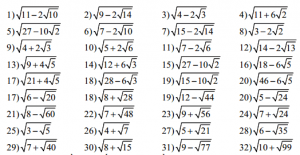
b) Rút gọn:

• Dạng cơ bản:

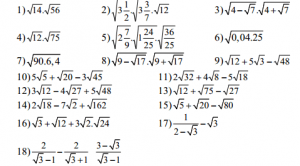
• Một số dạng nâng cao

 

 

Bài 2: Rút gọn biểu thức

a) Biểu thức không chứa ẩn:

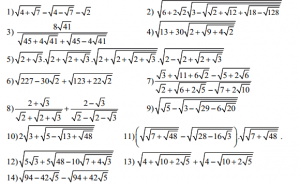
b) Biểu thức chứa ẩn:

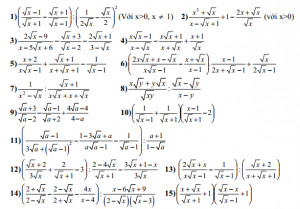
Bài 3: Cho x là một số nguyên tố, tìm x để các biểu thức sau có giá trị nguyên:

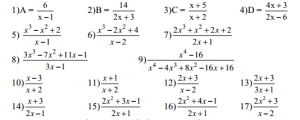
Lý thuyết: căn bậc hai- căn bậc 2
Dạng 1: So sánh căn bậc hai số học
Dạng 2: Tìm điều kiện để √A có nghĩa
Dạng 3: Rút gọn biểu thức chứa căn bậc hai (dạng √(A2))
Dạng 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn Xem chi tiết
Bài tập tổng hợp về Căn bậc hai

Lý thuyết: Căn bậc hai

1. Căn bậc hai số học

    – Căn bậc hai số học của số thực a không âm là số không âm x mà x² = a

    – Với a ≥ 0

x = √a 

Phép toán tìm căn bậc hai số học của một số gọi là phép khai phương

Với hai số a, b không âm, thì ta có: a < b ⇔ √a < √b

2. Căn thức bậc hai

    – Cho A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.

    – √A xác định (hay có nghĩa) khi A ≥ 0

    – Hằng đẳng thức √(A²)=|A|

3. Chú ý

       +) Với a ≥ 0 thì:

(√x = a ⇒ x = a²)

(x² = a ⇒ x = ±√a)

        +) √A = √B 

        +) √A + √B = 0 ⇔ A = B = 0

Bài viết lý thuyết và bài tập căn bậc hai – căn bậc 2 sẽ giải thích về căn bậc hai số học, căn bậc 2 của 2, khai căn bậc 2, bảng căn bậc 2, cách tính căn bậc 2, công thức căn bậc 2, dấu căn bậc 2…..