CÁC LOẠI NGUYÊN HÀM

• Gồm có 2 phần: Phần 1 – Tóm tắt lý thuyết, Phần 2 – Các loại nguyên hàm.
• Phần 1 tóm tắt lý thuyết về định nghĩa, định lí, tính chất, các công thức cơ bản,… và các link bài chi tiết về lí thuyết.
• Phần 2 các link bài chi tiết về lý thuyết và bài tập của hầu hết các loại nguyên hàm.

PHỤ HUYNH VÀ CÁC EM HỌC SINH CÓ THỂ TÌM HIỂU THÊM:

Nguyên hàm – Lý thuyết và bài tập

Các công thức nguyên hàm

Nguyên hàm từng phần

I. Tóm tắt lý thuyết:

1. Định nghĩa:

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên (a;b)nếu F′(x)=f(x)

Ví dụ:

• Hàm số y=x² là nguyên hàm của hàm số y=2x trên R vì (x²)′=2x

2. Định lý:

1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

• Do đó F(x) + C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C

3. Sự tồn tại của nguyên hàm:

• Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

4. Các tính chất:

5. Bảng công thức nguyên hàm của một số hàm số sơ cấp:

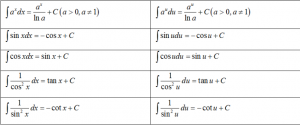
• Tìm hiểu thêm về các công thức nguyên hàm cơ bản và nâng cao ở đây.

II. Các loại nguyên hàm:

1. Nguyên hàm từng phần: https://www.nguyentheanh.com/nguyen-ham-tung-phan

2. Nguyên hàm 2 ẩn, 3 ẩn: https://www.nguyentheanh.com/nguyen-ham-2-3

3. Nguyên hàm lượng giác: https://www.nguyentheanh.com/nguyen-ham-luong-giac

4. Nguyên hàm hữu tỷ, vô tỷ: https://www.nguyentheanh.com/nguyen-ham-huu-ty-vo-ty

5. Nguyên hàm vận dụng cao: https://www.nguyentheanh.com/nguyen-ham-van-dung-cao

6. Các loại nguyên hàm đặc biệt: https://www.nguyentheanh.com/cac-loai-nguyen-ham-dac-biet