Các bài hình học lớp 9 vào 10 hay thi vào 2018.
Các bài hình học lớp 9 vào 10 hay thi vào 2018. Đây là những bài tập hình hay thi vào 10 được thầy Thế Anh tổng hợp và đưa ra lời giải. Hi vọng sẽ giúp các em học sinh và các quý phụ huynh có con em vào 10 đạt kết quả cao nhất.
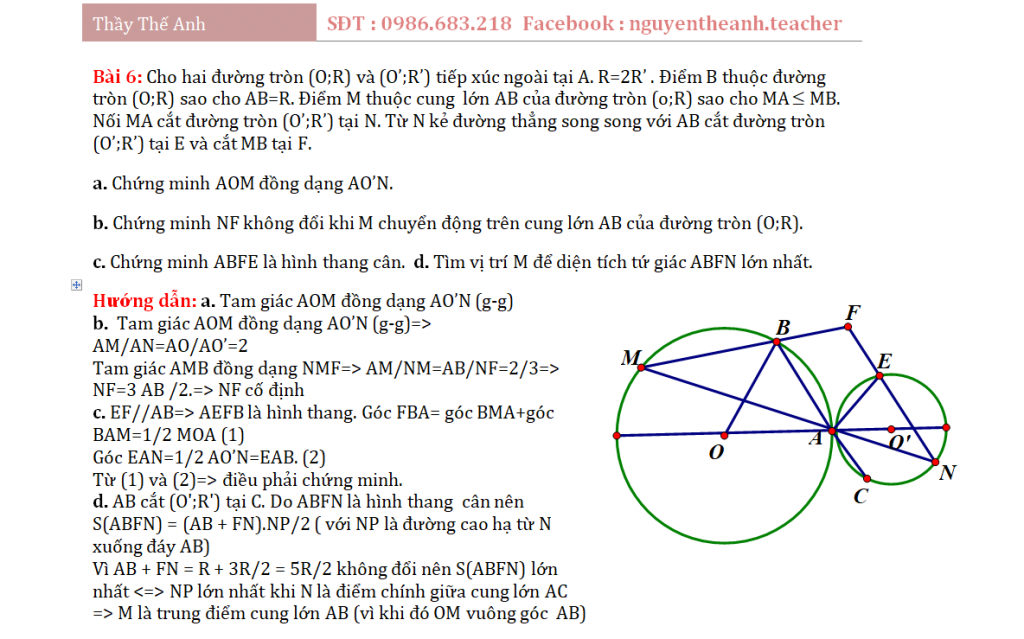
Bài 6: Cho hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài tại A. R=2R’ . Điểm B thuộc đường tròn (O;R) sao cho AB=R. Điểm M thuộc cung lớn AB của đường tròn (o;R) sao cho MAMB. Nối MA cắt đường tròn (O’;R’) tại N. Từ N kẻ đường thẳng song song với AB cắt đường tròn (O’;R’) tại E và cắt MB tại F.
-
Chứng minh AOM đồng dạng AO’N.
-
Chứng minh NF không đổi khi M chuyển động trên cung lớn AB của đường tròn (O;R).
-
Chứng minh ABFE là hình thang cân. d. Tìm vị trí M để diện tích tứ giác ABFN lớn nhất.
| Hướng dẫn: a. Tam giác AOM đồng dạng AO’N (g-g)
b. Tam giác AOM đồng dạng AO’N (g-g)=> AM/AN=AO/AO’=2 Tam giác AMB đồng dạng NMF=> AM/NM=AB/NF=2/3=> NF=3 AB /2.=> NF cố định c. EF//AB=> AEFB là hình thang. Góc FBA= góc BMA+góc BAM=1/2 MOA (1) Góc EAN=1/2 AO’N=EAB. (2) Từ (1) và (2)=> điều phải chứng minh. d. AB cắt (O’;R’) tại C. Do ABFN là hình thang cân nên S(ABFN) = (AB + FN).NP/2 ( với NP là đường cao hạ từ N xuống đáy AB) Vì AB + FN = R + 3R/2 = 5R/2 không đổi nên S(ABFN) lớn nhất <=> NP lớn nhất khi N là điểm chính giữa cung lớn AC => M là trung điểm cung lớn AB (vì khi đó OM vuông góc AB)
|
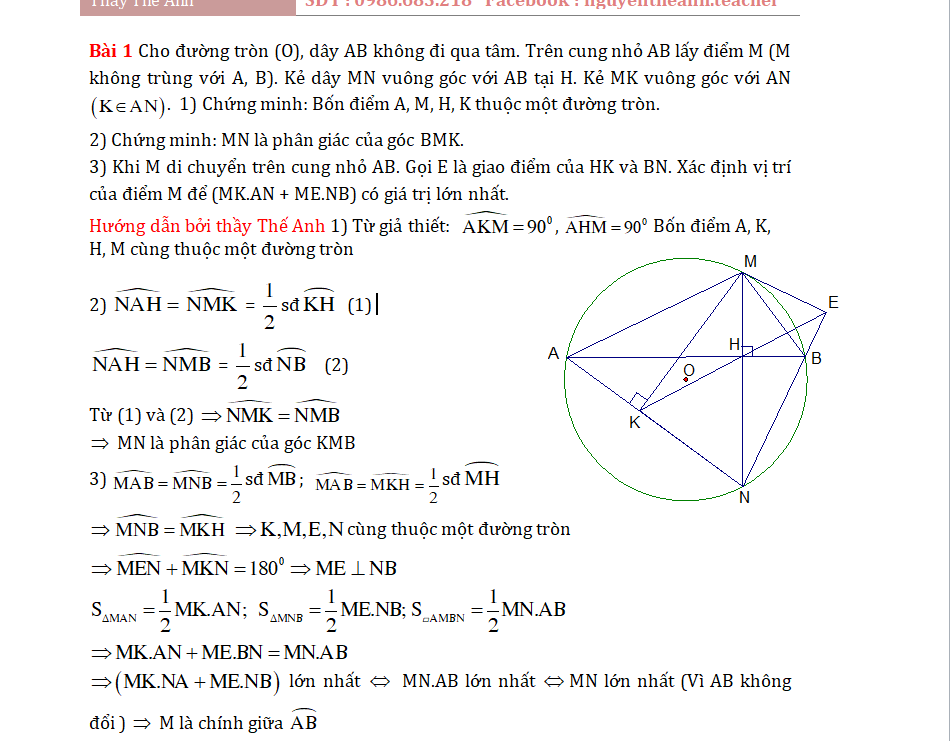
Bài 2: Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
1) Chứng minh: Bốn điểm A, M, H, K thuộc một đường tròn.
2) Chứng minh: MN là phân giác của góc BMK.
3) Khi M di chuyển trên cung nhỏ AB. Gọi E là giao điểm của HK và BN.
Xác định vị trí của điểm M để (MK.AN + ME.NB) có giá trị lớn nhất.
1) Từ giả thiết: ,
Bốn điểm A, K, H, M cùng thuộc một đường tròn
2) = sđ (1)
= sđ (2)
Từ (1) và (2)
MN là phân giác của góc KMB
3) sđ; sđ
cùng thuộc một đường tròn
lớn nhất MN.AB lớn nhất
MN lớn nhất (Vì AB= const ) M là chính giữa