BẤT PHƯƠNG TRÌNH CHỨA THAM SỐ M

• “Bất phương trình chứa tham số m” gồm có 2 phần: Phần 1 nhắc lại các kiến thức cần nhớ và Phần 2 là các phương pháp giải bất phương trình chứa tham số m.

PHỤ HUYNH VÀ HỌC SINH CÓ THỂ TÌM HIỂU THÊM:

Tất cả kiến thức về bất phương trình

Bất phương trình mũ

Bất phương trình logarit

I. Các kiến thức cần nhớ:

• Điều kiện để phương trình ax+b=0 có nghiệm, vô nghiệm trên (a;b); [a;b]; (a;+∞)
• Định lý Viét
• Điều kiện để phương trình ax2+bx+c=0

+) Có nghiệm

+) Vô nghiệm

+) Có 2 nghiệm âm.

+) Có 2 nghiệm dương

+) Có nghiệm x1 < x2 <a (đặt x-a = t đưa về bài toán 2 nghiệm âm)

+) Có nghiệm : a < x1 £   x2 ( đặt x-a = t đưa về bài toán 2 nghiệm dương)     

II. Các phương pháp giải bất phương trình chứa tham số m:

1.Phương pháp hàm số để giải bất phương trình chứa tham số m:

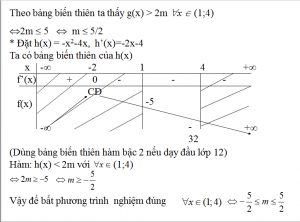
2. Phương pháp dùng điều kiện cần và đủ để giải bất phương trình chứa tham số m:

a- Kiến thức cần nhớ: 

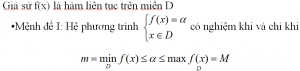
b- Định nghĩa:

 Xét mệnh đề A⇒B đúng thì A là điều kiện đủ để có B còn B là điều kiện cần để có A

c- Cách làm :

   Tìm tham số để phương trình (A) thỏa mãn tính chất T

• Điều kiện cần : (A) muốn thỏa mãn tính chất T thì (A) thỏa mãn ít nhất 1 tính chất t ∈ T.
• Điều kiện đủ: Với các tham số vừa tìm được, kiểm tra ( chứng minh) xem tham số nào để (A) có tính chất T.
• Kết luận.

3. Phương pháp biện luận bằng đồ thị để giải bất phương trình chứa tham số m:

a, Phương pháp:

• Xét bất phương trình  f(x )< g(x)  /D

    + Vẽ đồ thị y = f(x); y = g(x) trên cùng một hệ tọa độ (Oxy)

    +Tìm  phần đồ thị y = f(x) nằm phía dưới đồ thị y = g(x) trên D

    + Tìm hình chiếu của phần đó trên Ox ta được nghiệm của bất phương trình đã cho

• Hai chú ý quan trọng về bất phương trình :

Bất phương trình f(x) < g(x) có nghiệm đúng “xÎD Û đồ thị hàm số y = f(x) nằm hoàn toàn phía dưới đồ thị y = g(x) /D

Bất phương trình f(x) < g(x) có nghiệm trên D khi đồ thị y = f(x) không hoàn toàn nằm phía trên đồ thị y = g(x) /D

b, VD: