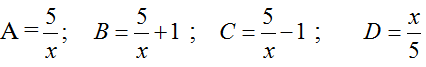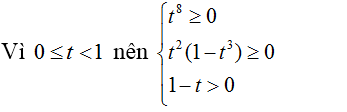1.Khái niệm bất đẳng thức

Trong toán học, một bất đẳng thức (tiếng Anh:Inequality) là một phát biểu về quan hệ thứ tự giữa hai đối tượng. (Xem thêm: đẳng thức)

• Ký hiệu {\displaystyle a<b\!\ } có nghĩa là a nhỏ hơn b
• Ký hiệu {\displaystyle a>b\!\ } có nghĩa là a lớn hơn b.

Những quan hệ nói trên được gọi là bất đẳng thức nghiêm ngặt; ngoài ra ta còn có

• {\displaystyle a\leq b} có nghĩa là a nhỏ hơn hoặc bằng b
• {\displaystyle a\geq b} có nghĩa là a lớn hơn hoặc bằng b.
• {\displaystyle |a|\geq a} có nghĩa là |a| lớn hơn hoặc bằng a.

Người ta còn dùng một ký hiệu khác để chỉ ra rằng một đại lượng lớn hơn rất nhiều so với một đại lượng khác.

• Ký hiệu a >>b có nghĩa là a lớn hơn b rất nhiều

Các ký hiệu a, b ở hai vế của một bất đẳng thức có thể là các biểu thức của các biến. Sau đây ta chỉ xét các bất đẳng thức với các biến nhận giá trị trên tập số thực hoặc các tập con của nó.

Nếu một bất đẳng thức đúng với mọi giá trị của tất cả các biến có mặt trong bất đẳng thức, thì bất đẳng thức này được gọi là bất đẳng thức tuyệt đối hay không điều kiện. Nếu một bất đẳng thức chỉ đúng với một số giá trị nào đó của các biến, với các giá trị khác thì nó bị đổi chiều hay không còn đúng nữa thì nó được goị là một bất đẳng thức có điều kiện. Một bất đẳng thức đúng vẫn còn đúng nếu cả hai vế của nó được thêm vào hoặc bớt đi cùng một giá trị, hay nếu cả hai vế của nó được nhân hay chia với cùng một số dương. Một bất đẳng thức sẽ bị đảo chiều nếu cả hai vế của nó được nhân hay chia bởi một số âm.

2. Tính chất của bất đẳng thức

Bất đẳng thức có các tính chất sau:

Tính chất bắc cầu

Tính chất bắc cầu của bất đẳng thức được phát biểu như sau:

• Với mọi số thực a, b,c:
  • Nếu a > b và b > c thì a > c
  • Nếu a < b và b < c thì a < c

Tính chất liên hệ đến phép cộng và phép trừ

Tính chất liên quan đến phép cộng và phép trừ được phát biểu như sau:

Phép cộng và phép trừ với cùng một số thực bảo toàn quan hệ thứ tự trên tập số thực. Nghĩa là

• Với mọi số thực a, b và c:
  • Nếu a > b thì a + c > b + c và a – c > b – c
  • Nếu a < b thì a + c < b + c và a – c < b – c

Tính chất liên hệ đến phép nhân và phép chia

Tính chất liên quan đến phép nhân và phép chia được phát biểu như sau:

Phép nhân (hoặc chia) với một số thực dương bảo toàn quan hệ thứ tự trên tập số thực, phép nhân (hoặc chia)với một số thực âm đảo ngược quan hệ thứ tự trên tập số thực. Cụ thể:

• Với mọi số thực a, b và c:
  • Nếu c là một số dương và a > b thì a × c > b × c và a/c > b/c
  • Nếu c là một số dương và a < b thì a × c < b × c và a/c < b/c
  • Nếu c là một số âm và a > b thì a × c < b × c và a/c < b/c
  • Nếu c là một số âm và a < b thì a × c > b × c và a/c > b/c

3. Phương pháp giải bài tập bất đẳng thức

A – PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG

Ví dụ 1: Chứng minh rằng:

                                $\frac{\sqrt{a}+\sqrt{b}}{2}<\sqrt{\frac{a+b}{2}}$     với $a>0;b>0;a\ne b$      (1)

Giải

$\left(1\right)\iff \frac{a+b+2\sqrt{ab}}{4}<\frac{a+b}{2}$

$\iff a+b+2\sqrt{ab}<2a+2b$

$\Leftrightarrow 0

$0<(\sqrt{a}-\sqrt{b}{)}^2$                     (2)

Do $a\ne b$ nên bất đẳng thức (2) đúng, vậy bất đẳng thức (1) được chứng minh.

Ví dụ 2: Chứng minh bất đẳng thức

                      $\sqrt{a^2+b^2}+\sqrt{c^2+d^2}\ge \sqrt{(a+c{)}^2+(b+d{)}^2}$                       (1)

Giải

 

$\left(1\right)\iff a^2+b^2+c^2+d^2+2\sqrt{(a^2+b^2)(c^2+d^2)}\ge a^2+c^2+2ac+b^2+d^2+2bd$

$\iff \sqrt{(a^2+b^2)(c^2+d^2)}\ge ac+bd$

Nếu ac + bd < 0 thì (2) được chứng minh

Nếu $ac+bd\ge 0$ thì (2) tương đương

                        $(a^2+b^2)(c^2+d^2)\ge a^2{c}^2+b^2{d}^2+2abcd$

                        $(ad-bc{)}^2\ge 0$                 (3)

Bất đẳng thức (3) đúng, vậy đẳng thức (1) được chứng minh.

B- PHƯƠNG PHÁP LÀM TRỘI, LÀM GIẢM

Ví dụ 3: Chứng minh bất đẳng thức sau với $n\in N,n\ge 2$

                  $2\sqrt{n}-3<\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{n}}<2\sqrt{n}-2$

Giải

Đặt $A=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{n}}$

a) Chứng minh $A>2\sqrt{n}-3$ bằng cách làm giảm mỗi số hạng của A

$\frac{1}{\sqrt{k}}=\frac{2}{\sqrt{k}+\sqrt{k}}>\frac{2}{\sqrt{k+1}+\sqrt{k}}=2(\sqrt{k+1}-\sqrt{k})$   với mọi $k\in$ N*

Do đó $A>2\left[\right(\sqrt{n+1}-\sqrt{n})+...+(\sqrt{4}-\sqrt{3})+(\sqrt{3}-\sqrt{2}\left)\right]=2(\sqrt{n+1}-\sqrt{2})=2\sqrt{n+1}-2\sqrt{2}>2\sqrt{n+1}-3>2\sqrt{n}-3.$

b) Chứng minh $A<2\sqrt{n}-2$ bằng cách làm trội mối số hạng của A

$\frac{1}{\sqrt{k}}=\frac{2}{\sqrt{k}+\sqrt{k}}<\frac{2}{\sqrt{k}+\sqrt{k-1}}=2(\sqrt{k}-\sqrt{k-1})$   với mọi $k\in$ N*

Do đó $A<2\left[\right(\sqrt{n}-\sqrt{n-1}\left)\right]+...+(\sqrt{3}-\sqrt{2})+(\sqrt{2}-\sqrt{1})=2(\sqrt{n}-\sqrt{1})=2\sqrt{n}-2$

C- PHƯƠNG PHÁP SỬ DỤNG CÁC BẤT ĐẲNG THỨC ĐÃ BIẾT

Ta nhắc lại ở đây ba bất đẳng thứ quan trọng

1. Tổng của hai số nghịch đảo nhau

                          $\frac{x}{y}+\frac{y}{x}\ge 2$ với x, y là hai số cùng dấu

2. Bất đẳng thức Cô-si 

Cho a, b, c là các số không âm. Khi đó:

                                             $\frac{a+b}{2}\ge \sqrt{ab}$

                                             $\frac{a+b+c}{3}\ge \sqrt[3]{3abc}$

Tổng quát: Trung bình cộng của n số không âm lớn hơn hoặc trung bình nhân của chúng

$\frac{a_1+a_2+...+a_n}{n}\ge \sqrt[n]{n{a}_1.a_2...a_n}$ với $a_1,a_2,...,a_n$ là các số không âm.

Đẳng thức xảy ra khi và chỉ khi  $a_1=a_2=...=a_n$

3. Bất đẳng thức Bu-nhi-a-cốp-xki 

 Cho hai bộ số a, b, c và x, y, z. Khi đó:

                                      $(a^2+b^2)(x^2+y^2)\ge (ax+by{)}^2$

                                 $(a^2+b^2+c^2)(x^2+y^2+z^2)\ge (ã+by+cz{)}^2$

Tổng quát: Có hai bộ n số: $(a_1,a_2,...,a_n)$ và $(b_1,b_2,...,b_n)$.Tích của tổng các bình phương n số của bộ số này và tổng các bình phương n số của bộ số kia lớn hơn hoặc bằng bình phương của tổng n tích hai số tương ứng của hai bộ số đó.

$(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)\ge (a_1{b}_1+a_2{b}_2+...+a_n+b_n{)}^2$

Đẳng thức xảy ra khi và chỉ khi $(a_1,a_2,...,a_n)$ và  $(b_1,b_2,...,b_n)$ là hai bộ số tỉ lệ với nhau tức là $\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$ với quy ước rằng nếu mẫu bằng 0 thì tử bằng 0.

Chứng minh

Đặt $A=a_1^2+a_2^2+...+a_n^2,B=b_1^2+b_2^2+...+b_n^2,C=a_1{b}_1+a_2{b}_2+...+a_n{b}_n$. Cần chứng minh $AB\ge C^2$

 

Nếu A = 0 thì $a_1=a_2=...=a_n$, bất đẳng thức được chứng minh. Cũng vậy nếu B = 0. Do đó ta chỉ cần xét trường hợp A và B khác 0

Với mọi x ta có:

$(a_{1}x-b_1{)}^2\ge 0\Rightarrow a_1^2{x}^2-2a_1{b}_{1}x+b_1^2\ge 0$

$(a_{2}x-b_2{)}^2\ge 0\Rightarrow a_2^2{x}^2-2a_2{b}_{2}x+b_2^2\ge 0$

…

$(a_{n}x-b_n{)}^2\ge 0\Rightarrow a_n^2{x}^2-2a_n{b}_{n}x+b_n^2\ge 0$

Cộng từng vế n bất đẳng thức trên được 

$(a_1^2+a_2^2+...+a_n^2)x^2-2(a_1{b}_1+a_2{b}_2+...+a_n{b}_n)x+(b_1^2+b_2^2+...+b_n^2)\ge 0$

tức là                                               $A{x}^2-2Cx+B\ge 0$                               (1)

Vì (1) đúng với mọi x nên thay $x=\frac{C}{A}$vào (1) ta được

$A.\frac{C^2}{A^2}-2.\frac{C^2}{A}+B\ge 0\Rightarrow B-\frac{C^2}{A}\ge 0\Rightarrow AB-C^2\ge 0\Rightarrow AB\ge C$

Xảy ra đẳng thức khi và chỉ khi $a_{1}x=b_1,a_{2}x=b_2,...,a_{n}x=b_n$ tức là $\frac{a_1}{b_1}=\frac{a_2}{b_2}=...=\frac{a_n}{b_n}$ với quy ước rằng nếu mẫu bằng 0 thì tử phải bằng 0

Ví dụ 4: Co a, b, c là các số dương. Chứng minh bất đẳng thức:

                                    $\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^b}{a+b}\ge \frac{a+b+c}{2}$

Giải

Cách 1. Theo bất đẳng thức Cô-si ta có:

                $\frac{a^2}{b+c}+\frac{b+c}{4}\ge 2\sqrt{\frac{a^2}{b+c}.\frac{b+c}{4}}=2.\frac{a}{2}=a$

 Suy ra  $\frac{a^2}{b+c}\ge a-\frac{b+c}{4}$

Tương tự $\frac{b^2}{a+c}\ge b-\frac{a+c}{4}$; $\frac{c^2}{a+b}\ge c-\frac{a+b}{4}$

Cộng từng vế của ba bất đẳng thức ta được

 $\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^b}{a+b}\ge (a+b+c)-\frac{a+b+c}{2}=\frac{a+b+c}{2}$

Cách 2. Theo bất đẳng thức Bu-nhi-a-cốp-xki ta có

 $\left[{\left(\frac{a}{\sqrt{b+c}}\right)}^2+{\left(\frac{b}{\sqrt{a+c}}\right)}^2+{\left(\frac{c}{\sqrt{a+b}}\right)}^2\right].\left[\right(\sqrt{b+c}{)}^2+(\sqrt{a+c}{)}^2+(\sqrt{a+b}{)}^2]$

$\ge {\left(\frac{a}{\sqrt{b+c}}.\sqrt{b+c}+\frac{b}{\sqrt{a+c}}.\sqrt{a+c}+\frac{c}{\sqrt{a+b}}.\sqrt{a+b}\right)}^2$

$\Rightarrow \left(\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\right)\left[2\right(a+b+c\left)\right]\ge (a+b+c{)}^2$

$\Rightarrow$ $\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^b}{a+b}\ge \frac{a+b+c}{2}$

Ví dụ 5. Cho a, b, c là các số không âm và a + b + c = 1. Chứng minh:

$a)\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<3,5$

$b)\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\le \sqrt{6}$

 Giải

 a) .Áp dụng bất đẳng thức Cô-si ta có

                              $\sqrt{a+1}=\sqrt{1(a+1)}\le \frac{(a+1)+1}{2}=\frac{a}{2}+1$

Tương tự :  $\sqrt{b+1}\le \frac{b}{2}+1$; $\sqrt{c+1}\le \frac{c}{2}+1$

Cộng từng vế ba bất đẳng thức trên ta được

        $\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}\le \frac{a+b+c}{2}+3=3,5$

Dấu “=” xảy ra khi và chỉ khi a + 1 = b + 1 = c + 1 = 1 $\iff$  a = b = c = 0, Trái với giả thiết a + b + c = 1

 Vậy $\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<3,5$

b) 

Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki, có:

$(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}{)}^2\le 3(a+b+b+c+c+a)=3.2=6$

$\Rightarrow$ $\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\le \sqrt{6}$

D – PHƯƠNG PHÁP PHẢN CHỨNG

Ví dụ 6. Cho a + b = 2. Chứng minh rằng

                                             $\sqrt[3]{3a}+\sqrt[3]{3b}\le 2$

Giải

Đặt $\sqrt[3]{3a}=m$; $\sqrt[3]{3b}=n$. Ta có $m^3+n^3\le 2$

Cần chứng minh $m+n\le 2$

Giả sử m + n > 2 thì 

  $(m+n{)}^3>8\Rightarrow m^3+n^3+3mn(m+n)>8\Rightarrow 2+3mn(m+n)>8\Rightarrow mn(m+n)>2\Rightarrow mn(m+n)>m^3+n^3$

Chia hai vế cho số dương m + n ta có

              $mn>m^2-mn+n^2\Rightarrow 0>(m-n{)}^2$    (vô lí)

Vậy $m+n\le 2$

 

E- PHƯƠNG PHÁP QUY NẠP TOÁN HỌC

Ví dụ 7. Chứng minh rằng $\frac{a_1+a_2+...+a_n}{n}\ge \sqrt[n]{n{a}_1{a}_2...a_n}$

Giải

Hiển nhiên mệnh đề dúng với n = 2

Giả sử mệnh đề đúng với n = k. Ta sẽ chứng minh mệnh đề cũng đúng với n = k + 1

Giả sử $a_1\le a_2\le ...\le a_k\le a_{k+1}$ thì $a_{k+1}\ge \frac{a_1+a_2+...+a_k}{k}$

Đặt $\frac{a_1+a_2+...+a_k}{k}=x$ thì $x\ge 0$, ta có $a_{k+1}=x+y$ với $y\ge 0$ và 

$x^k\ge a_1{a}_2...a_k$ (do giả thiết quy nạp). Ta có:

${\left(\frac{a_1+a_2+...+a_k+a_{k+1}}{k+1}\right)}^{k+1}={\left(\frac{kx+x+y}{k+1}\right)}^{k+1}={\left(x+\frac{y}{k+1}\right)}^{k+1}\ge x^{k+1}+(k+1).\frac{y}{k+1}.x^k=x^{k+1}+x^{k}y=k^k(x+y)\ge a_1{a}_2...a_k{a}_{k+1}$

Suy ra  $\frac{a_1+a_2+...+a_k+a_{k+1}}{k+1}\ge \sqrt[k+1]{k+1a_1{a}_2...a_{k+1}}$

Vậy mệnh đề đúng với mọi số tự nhiên $n\ge 2$

Xảy ra đẳng thức khi và chỉ khi $a_1=a_2=...a_n$

4. Các bài tập đặc trưng

Bài 1: Chứng minh các bất đẳng thức sau:

 

$a)x^2+x\sqrt{2}+1>0$

$b)\sqrt{a+b}+\sqrt{a-b}<2\sqrt{a}$ với a > b > 0

 

Bài 2: Chứng minh các bất đẳng thức sau:

 

$a\left)\right(x+y+z{)}^2\le 3(x^2+y^2+z^2)$

$b)a^3+b^3+abc\ge ab(a+b+c)$ với các số dương a, b, c

 

Bài 3. Cho $a=\sqrt{2004}-\sqrt{2003},b=\sqrt{2005}-\sqrt{2004}$

So sánh a và b

 

Bài 4. Cho $A=\frac{1}{\sqrt{1.1999}}+\frac{1}{\sqrt{2.1998}}+\frac{1}{\sqrt{3.1997}}+...+\frac{1}{\sqrt{1999.1}}$

CMR: A > 1.999

 

Bài 5: Chứng minh với mọi số nguyên dương n:

 

$a)\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}\frac{1}{4\sqrt{3}+3\sqrt{4}}+...+\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1}}<1$

$b)\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+...+\frac{1}{(n+1)\sqrt{n}}<2$

 

Bài 6: Chứng minh với mọi số tự nhiên $n\ge 2$ đều có

            $\sqrt{n}<\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+...+\frac{1}{\sqrt{n}}<2\sqrt{n}$

 

Bài 7: Cho 25 số tự nhiên  $a_1,a_2,...,a_{25}$ thỏa mã điều kiện

               $\frac{1}{\sqrt{a_1}}+\frac{1}{\sqrt{a_2}}+\frac{1}{\sqrt{a_3}}+...+\frac{1}{\sqrt{a_{25}}}=9$ 

Chứng minh rằng trong 25 số tự nhiên đó, tồn tại hai số bằng nhau

 

Bài 8: Chứng minh với mọi số nguyên dương n

          $\sqrt{1}+\sqrt{2}+\sqrt{3}+...+\sqrt{n}\le n\sqrt{\frac{n+1}{2}}$

 

Bài 9: Cho $a=\frac{\sqrt{2}-\sqrt{1}}{1+2}+\frac{\sqrt{3}-\sqrt{2}}{2+3}+\frac{\sqrt{4}-\sqrt{3}}{3+4}+...+\frac{\sqrt{25}-\sqrt{24}}{24+25}$

Chứng minh rằng $a<\frac{2}{5}$

 

Bài 10: Cho $A=\frac{1}{2}.\frac{3}{4}.\frac{5}{6}...\frac{2n-1}{2n}$         $(n\in N,n\ge 2)$

Chứng minh rằng 

$a)A<\frac{1}{\sqrt{2n+1}}$

$b)A<\frac{1}{\sqrt{3n+1}}$

5. Giải bài tập trong SBT lớp 10.

Bài 1 (trang 79 SGK Đại Số 10): Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?

a) 8x > 4x ;     b) 4x > 8x

c) 8x² > 4x² ;     d) 8 + x > 4 + x

Lời giải

a) chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a) sai)

b) chỉ đúng khi x < 0

c) chỉ đúng khi x ≠ 0

d) đúng với mọi x.

Vậy khẳng định d là đúng với mọi giá trị của x.

Bài 2 (trang 79 SGK Đại Số 10): Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?

Lời giải

Bài 3 (trang 79 SGK Đại Số 10): Cho a, b, c là độ dài ba cạnh của một tam giác.

a) Chứng minh (b – c)² < a²

b) Từ đó suy ra: a² + b² + c² < 2(ab + bc + ca)

Lời giải

a) Vì a, b, c là độ dài 3 cạnh của một tam giác nên: a, b, c > 0; a + b + c > 0 và a + b – c > 0

Do đó: a² – (b – c)² = (a + b – c)(a – b + c) > 0

⇒ a² > (b – c)²

Vậy (b – c)² < a² (1) (đpcm)

b) Tương tự từ a) ta cũng có:

(c – a)² < b² (2) và (a – b)² < c² (3)

Cộng vế theo vế của (1), (2) và (3) ta được:

(b – c)² + (c – a)² + (a – b)² < a² + b² + c²

⇒ 2(a² + b² + c²) – 2(ab + bc + ca) < a² + b² + c²

⇒ a² + b² + c² < 2(ab + bc + ca) (đpcm)

Bài 4 (trang 79 SGK Đại Số 10): Chứng minh rằng:

x³ + y³ ≥ x²y + xy², ∀x, y ≥ 0

Lời giải

Ta có: (x – y)² ≥ 0 ⇔ x² + y² – 2xy ≥ 0

⇔ x² + y² – xy ≥ xy

Do x ≥ 0, y ≥ 0 ⇒ x + y ≥ 0

Ta có: (x + y)(x² + y² – xy) ≥ (x + y)xy

⇔ x³ + y³ ≥ x²y + xy² (đpcm)

Bài 5 (trang 79 SGK Đại Số 10): Chứng minh rằng:

x⁴ – √x⁵ + x – √x + 1 > 0, ∀ x ≥ 0

Lời giải

Đặt t = √x (điều kiện t ≥ 0), ta có:

x⁴ – √x⁵ + x – √x + 1 = t⁸ – t⁵ + t² – t + 1 = f(t)

– Khi 0 ≤ x < 1 ⇒ 0 ≤ t < 1

⇒ f(t) > 0 (*)

– Khi x ≥ 1 ⇒ t ≥ 1 ta có:

f(t) = t⁵(t³ – 1) + (t² – t + 1)

Từ (*) và (**) suy ra: x⁴ – √x⁵ + x – √x + 1 > 0, ∀ x ≥ 0 (đpcm)