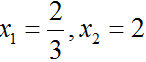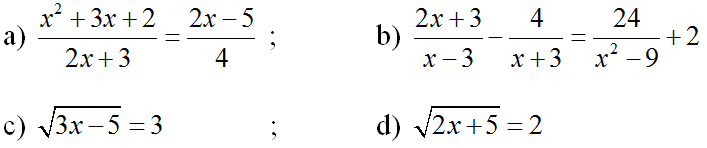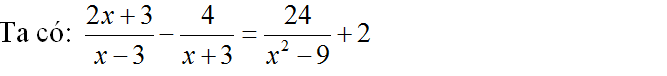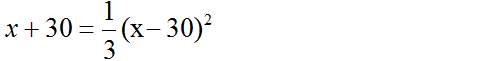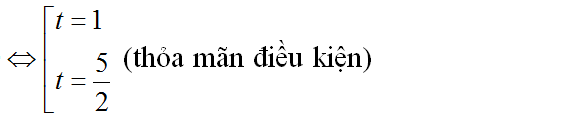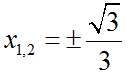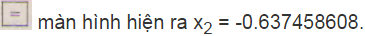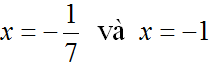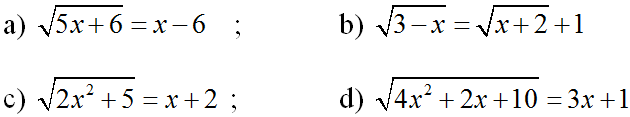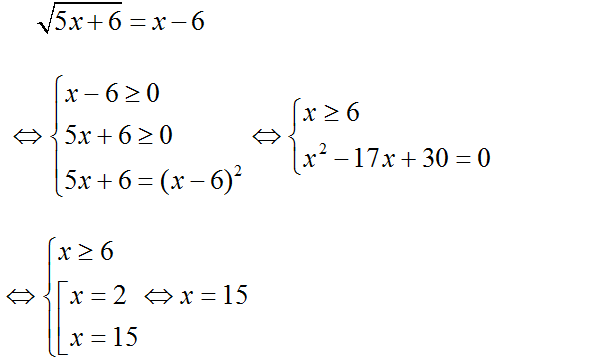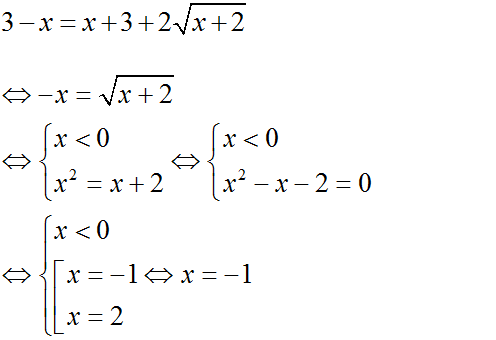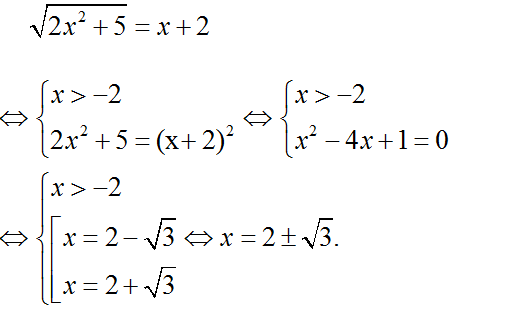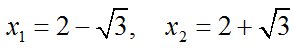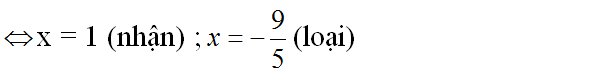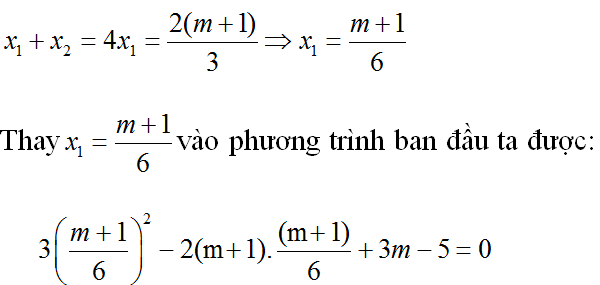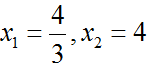Bài 2 (trang 62 SGK Đại số 10): Giải và biện luận các phương trình sau theo tham số m:

a) m(x – 2) = 3x + 1 ;

b) m²x + 6 = 4x + 3m ;

c) (2m + 1)x – 2m = 3x – 2.

Lời giải:

a) m(x – 2) = 3x + 1

⇔ (m – 3)x = 1 + 2m     (1)

– Nếu m – 3 ≠ 0 ⇔ m ≠ 3 thì phương trình (1) có nghiệm duy nhất

– Nếu m – 3 = 0 ⇔ m = 3 thì (1) ⇔ 0x = 7

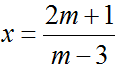
=> phương trình vô nghiệm

b) m²x + 6 = 4x + 3m

⇔ (m² – 4)x = 3m – 6     (2)

– Nếu m² – 4 ≠ 0 ⇔ m ≠ ±2 thì phương trình có nghiệm duy nhất

– Nếu m² – 4 = 0 ⇔ m = ±2

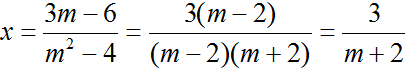
    + Với m = 2 thì (2) ⇔ 0x = 0 => phương trình có vô số nghiệm

    + Với m = -2 thì (2) ⇔ 0x = -12 => phương trình vô nghiệm

c) (2m + 1)x – 2m = 3x – 2

⇔ 2mx + x – 2m – 3x + 2 = 0

⇔ 2mx – 2x – 2m + 2 = 0

⇔ (m – 1)x – (m – 1) = 0

⇔ (m – 1)(x – 1) = 0

– Nếu m – 1 ≠ 0 ⇔ m ≠ 1 thì (3) tương đương với:

x – 1 = 0 => x = 1

– Nếu m – 1 = 0 ⇔ m = 1 thì (3) ⇔ 0x = 0

=> phương trình có vô số nghiệm

Bài 3 (trang 62 SGK Đại số 10): Có hai rổ quýt chứa số quýt bằng nhau. Nếu lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ hai bằng 1/3 của bình phương số quả còn lại ở rổ thứ nhất. Hỏi số quả quýt ở mỗi rổ lúc ban đầu là bao nhiêu?

Lời giải:

Gọi x là số quýt ở mỗi rổ (x > 30; x ∈ N).

Khi lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì:

– Rổ thứ nhất còn x – 30 (quả)

– Rổ thứ hai có x + 30 (quả)

Theo đề bài ta có phương trình:

⇔ 3(x + 30) = (x – 30)²

⇔ x² – 63x + 810 = 0

⇔ x = 18 (loại) hoặc x = 45 (thỏa mãn)

Vậy ban đầu mỗi rổ có 45 quả quýt

Bài 4 (trang 62 SGK Đại số 10): Giải các phương trình

a) 2x⁴ – 7x² + 5 = 0 ;         b) 3x⁴ + 2x² – 1 = 0

Lời giải:

a) 2x⁴ – 7x² + 5 = 0 (1)

Đặt t = x² (Điều kiện: t ≥ 0)

Khi đó (1) ⇔ 2t² – 7t + 5 = 0

– Với t = 1 ta có: x² = 1 ⇔ x = ±1

b) 3x⁴ + 2x² – 1 = 0 (2)

Đặt t = x² (Điều kiện: t ≥ 0)

Khi đó (2) ⇔ 3t² + 2t – 1 = 0

Vậy phương trình có hai nghiệm:

Bài 5 (trang 62 SGK Đại số 10): Giải các phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ ba)

a) 2x² – 5x – 4 = 0 ;         b) -3x² + 4x + 2 = 0

c) 3x² + 7x + 4 = 0 ;         d) 9x² – 6x – 4 = 0.

Hướng dẫn cách giải câu a): Nếu sử dụng máy tính CASIO fx-500 MS, ta ấn liên tiếp các phím

màn hình hiện ra x₁ = 3.137458609

Ấn tiếp

Làm tròn kết quả đến chữ số thập phân thứ ba ta được nghiệm gần đúng của phương trình là x₁≈ 3.137 và x₂ ≈ -0.637.

Lời giải:

a) Cách giải ở trên, kết quả:

    x₁ ≈ 3.137 và x₂ ≈ -0.637

b) Ấn liên tiếp các phím

và sau đó ấn phím =.

Kết quả làm tròn: x₁ ≈ 1,721 và x₂ ≈ 0,387

c) Ấn liên tiếp các phím

và sau đó ấn phím =.

Kết quả làm tròn: x₁ ≈ -1 và x₂ ≈ -1,333

d) Ấn liên tiếp các phím

và sau đó ấn phím =.

Kết quả đã làm tròn: x₁ ≈ 1,079 và x₂ ≈ -0,412

Bài 6 (trang 62-63 SGK Đại số 10): Giải các phương trình

a) |3x – 2| = 2x + 3 ;

b) |2x – 1| = |-5x – 2| ;

d) |2x + 5| = x² + 5x + 1.

Lời giải:

a) |3x – 2| = 2x + 3     (1)

Khi đó (1) ⇔ 3x – 2 = 2x + 3

⇔ x = 5 (nhận)

Khi đó (1) ⇔ 2 – 3x = 2x + 3

⇔ 5x = -1

Vậy phương trình có hai nghiệm là:

b) |2x – 1| = |-5x – 2|

Vậy phương trình có hai nghiệm là:

c) Điều kiện:

⇔ |x + 1|(x – 1) = -6x² + 11x – 3     (3)

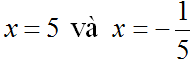
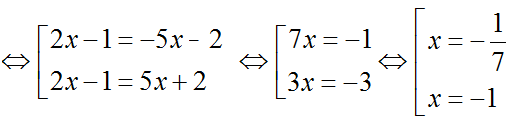
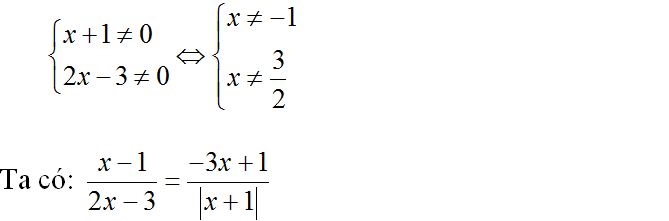
– Nếu x + 1 > 0 ⇔ x > -1

Khi đó (3) ⇔ x² – 1 = -6x² + 11x – 3

⇔ 7x² – 11x + 2 = 0

– Nếu x + 1 < 0 ⇔ x < -1

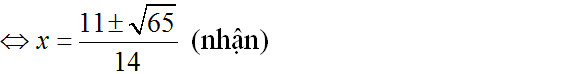
Khi đó (3) ⇔ 1 – x²= -6x² + 11x – 3

⇔ 5x² – 11x + 4 = 0

Vậy phương trình có hai nghiệm:

d) |2x + 5| = x² + 5x + 1     (4)

Khi đó (4) ⇔ 2x + 5 = x² + 5x + 1

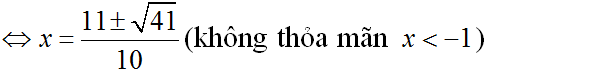
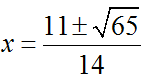
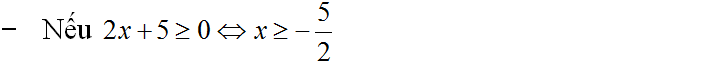
⇔ x² + 3x – 4 = 0

⇔ x = 1 (nhận) ; x = -4 (loại)

Khi đó (4) ⇔ -2x – 5 = x² + 5x + 1

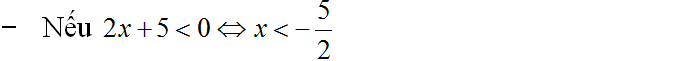
⇔ x² + 7x + 6 = 0

⇔ x = -6 (nhận) ; x = -1 (loại)

Vậy phương trình có hai nghiệm: x = 1 ; x = -6.

Bài 7 (trang 63 SGK Đại số 10): Giải các phương trình

Lời giải:

a)

Vậy phương trình có nghiệm x = 15.

b) Điều kiện: -2 ≤ x ≤ 3

Bình phương hai vế của phương trình ta được:

Vậy phương trình có nghiệm x = -1.

c)

Vậy phương trình có hai nghiệm:

d) Điều kiện:

Bình phương hai vế của phương trình ta được:

4x² + 2x + 10 = (3x + 1)²

4x² + 2x + 10 = 9x² + 6x + 1

5x² + 4x – 9 = 0

Vậy phương trình có nghiệm x = 1.

 

Bài 8 (trang 63 SGK Đại số 10): Cho phương trình 3x² – 2(m + 1)x + 3m – 5 = 0

Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.

Lời giải:

Giả sử phương trình có 2 nghiệm x₁ và x₂ với x₂ = 3x₁

Theo định lí Vi-ét ta có:

⇔ -3m² + 30 m – 63 = 0

⇔ m² – 10 m + 21 = 0

⇔ m₁ = 3 ; m₂ = 7

– Thay m = 3 vào x₁, x₂ ở trên ta được hai nghiệm là:

– Thay m = 7 vào x₁, x₂ ở trên ta được hai nghiệm là: