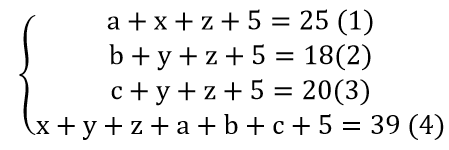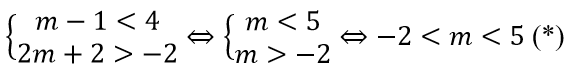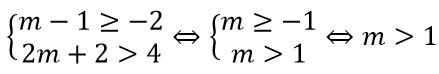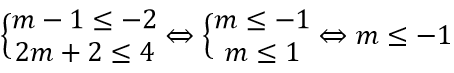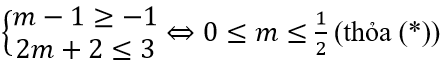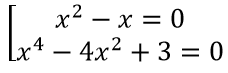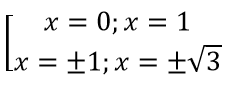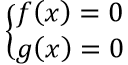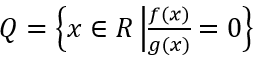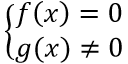Bài tập mệnh đề và tập hợp có đáp án
Duới đây là một số bài tập giúp các bạn ôn tập lại phần mệnh đề quan hệ được học trong phần đầu chương trình lớp 10. Các bài tập được phân loại ở mức độ cơ bản và đi từ tự luận tới trắc nghiệm.
- Mệnh đề tập hợp
- Bài tập mệnh đề và tập hợp có đáp án
- Chuyên đề mệnh đề tập hợp toán 10
- Bài tập mệnh đề tập hợp nâng cao
- Ôn tập mệnh đề tập hợp
- Lý thuyết và bài tập mệnh đề tập hợp
- 100 câu trắc nghiệm mệnh đề tập hợp
1.Một số bài tập tự luận
Bài 1: Phát biểu nào sau đây là mệnh đề:
a) Phở là một món ăn của người Việt Nam
b) Hôm qua, trời đẹp quá.
c) 6 : 2 = 5 – 3
d) 6 – 2 = 3 + 5
e) 3 ≥ 4
Bài 2: Xác định tính đúng sai của các mệnh đề sau:
a) 2007 là số nguyên tố
b) Phương trình x2 – 3x + 2 =0 vô nghiệm
c) ∀n ∈ N,n2 – n chia hết cho 2
d) ∀x ∈ R,x2 – 2x + 2 > 0.
Bài 3: Cho mệnh đề: “Nếu tam giác cân thì nó có hai đường trung tuyến bằng nhau”.
a) Chứng minh mệnh đề trên đúng
b) Phát biểu mệnh đề trên dùng thuật ngữ “điều kiện cần”
c) Phát biểu mệnh đề trên dùng thuật ngữ “điều kiện đủ”
d) Phát biểu mệnh đề đảo của mệnh đề trên và cho biết mệnh đề đảo đúng hay sai.
Bài 4: Cho Oxy, lập mệnh đề kéo theo và mệnh đề tương đương của hai mệnh đề sau đây và cho biết tính đúng, sai của chúng:
P: “Điểm M nằm trên phân giác của góc Oxy”.
Q: “Điểm M cách đều hai cạnh Ox, Oy”
Bài 5: Cho A={n|n ∈ N,n ≤ 3}
B = {x ∈ R|x(x – 1)(x – 2)(x – 3)(x – 4)= 0};
C = {2n|n ∈ Z,-1 ≥ n ≥ 2}.
Liệt kê các phần tử của A, B, C.
Xác định các tập hợp sau và so sánh:
a) (A ∪ B) ∪ C;A ∪ (B ∪ C)
b) (A ∩ B) ∩ C;A ∩ (B ∩ C)
c) A ∪ (B ∩ C); (A ∪ B) ∩ (A ∪ C)
d) A ∩ (B ∪ C); (A ∩ B) ∪ (A ∩ C)
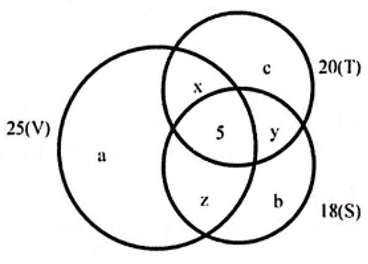
Bài 6: Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn văn, 20 em thích môn toán, 18 em thích môn sử, 6 em ko thích môn nào, 5 em thích cả 3 môn. Hỏi số em chỉ thích một môn trong ba môn trên.
Bài 7: Cho hai tập khác rỗng : A=(m – 1;4], B=(-2;2m + 2), với m ∈ R . Xác định m để:
| a) A ∩ B= ∅ ; | b) A ⊂ B; |
| c) B ⊂ A | D) (A ∩ B) ⊂ (-1;3) |
Bài 8: giả sử biết số đúng là 3,258. Tìm sai số tuyệt đối khi quy tròn số này đến hàng phần trăm.
Bài 9: Hãy viết số quy tròn của số a với độ chính xác d được cho sau đây:
a) a− = 17658 ± 36;
b) (a)−−−= 15318 ± 0,046.
Đáp án và hướng dẫn giải
Bài 1:
Các phát biểu là mệnh đề: a, c, d, e.
Phát biểu không là mệnh đề: b
Bài 2:
a) 2007 là số nguyên tố
Mệnh đề sai, vì 2007 ngoài ước là 1, 2007 còn ước 3; 9.
b) Phương trình x2 – 3x + 2=0 vô nghiệm
Mệnh đề sai vì phương trình có 2 nghiệm x = 1; x = 2
c) ∀n ∈ N,n2 – n chia hết cho 2
n2 – n=n(n – 1) đây là tích của 2 số liên tiếp nên chia hết cho 2.
⇒ Mệnh đề đúng.
d) ∀x ∈ R,x2 – 2x + 2 > 0.
x2 – 2x + 2 =(x – 1)2 + 1 > 0 ∀x ∈ R.
⇒ Mệnh đề đúng.
Bài 3: “Nếu tam giác cân thì nó có hai đường trung tuyến bằng nhau”.
Q = “Tam giác ABC có hai trung tuyến bằng nhau”
Khi đó mệnh đề đã cho có dạng “P ⇒ Q”
Ta thấy: nếu P đúng thì Q cũng đúng, nên “P ⇒ Q” là mệnh đề đúng.
b)”Tam giác có hai trung tuyến bằng nhau là điều kiện cần để tam giác đó cân”.
c)”Tam giác cân là điều kiện đủ đề tam giác đó có 2 trung tuyến bằng nhau”.
d) Mệnh đề đảo: “Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó cân”.
Mệnh đề đảo đúng.
Bài 4:
P ⇒ Q: “Nếu điểm M nằm trên phân giác của góc Oxy thì M cách đều hai cạnh Ox, Oy”: đúng.
Q ⇒ P: “Điểm M cách đều hai cạnh Ox, Oy thì M nằm trên phân giác của góc Oxy”: đúng.
P Q: “Điểm M nằm trên phân giác của góc Oxy nếu và chỉ nếu (khi và chỉ khi) điểm M cách đều hai cạnh Ox, Oy” : đúng.
Hay : P Q : “Điều kiện cần và đủ để điểm M nằm trên phân giác của góc Oxy là M cách đều hai cạnh Ox, Oy” : đúng.
Bài 5: Cho A={n|n ∈ N,n ≤ 3}
B={x ∈ R|x(x – 1)(x – 2)(x – 3)(x – 4)= 0};
C={2n|n ∈ Z,-1 ≤ n ≤ 2}.
Liệt kê các phần tử của A, B, C.
Xác định các tập hợp sau và so sánh:
a) (A ∪ B) ∪ C;A ∪ (B ∪ C)
b) (A ∩ B) ∩ C;A ∩ (B ∩ C)
c) A ∪ (B ∩ C); (A ∪ B) ∩ (A ∪ C)
d) A ∩ (B ∪ C); (A ∩ B) ∪ (A ∩ C)
A={n|n ∈ N,n ≤ 3}
⇒ A={0;1;2;3}
B={x ∈ R|x(x – 1)(x – 2)(x – 3)(x – 4)=0}
⇒ B={0;1;2;3;4}
C={2n|n ∈ Z,-1 ≤ n ≤ 2}
⇒ C={-2;0;2;4}
a) A ∪ B={0;1;2;3;4}
⇒ (A ∪ B) ∪ C={-2;0;1;2;3;4}
B ∪ C={-2;0;1;2;3;4}
⇒ A ∪ (B ∪ C)={-2;0;1;2;3;4}
Vậy (A ∪ B) ∪ C= A ∪ (B ∪ C)
b) A ∩ B={0;1;2;3}
⇒ (A ∩ B) ∩ C={0;2}
B ∩ C={0;2;4}
⇒ A ∩ (B ∩ C)={0;2}
Vậy (A ∩ B) ∩ C= A ∩ (B ∩ C)
c) A ∪ (B ∩ C)={0;1;2;3} ∪ {0;2;4}={0;1;2;3;4}
A ∪ C={-2;0;1;2;3;4}
(A ∪ B) ∩ (A ∪ C)={0;1;2;3;4} ∩ {-2;0;1;2;3;4}={0;1;2;3;4}
Vậy A ∪ (B ∩ C)=(A ∪ B) ∩ (A ∪ C).
d) A ∩ (B ∪ C)={0;1;2;3} ∩ {0;2;4}={0;2}
A ∩ C={0;2}
(A ∩ B) ∪ (A ∩ C)={0;1;2;3} ∪ {0;2}={0;2}
Vậy A ∩ (B ∪ C)=(A ∩ B) ∪ (A ∩ C)
Bài 6:
Gọi a,b,c theo thứ tự là số học sinh chỉ thích môn văn, sử, toán;
x là số học sinh chỉ thích hai môn văn và toán
y là số học sinh chỉ thích hai môn sử và toán
z là số học sinh chỉ thích hai môn văn và sử
Ta có số em thích ít nhất một môn là 45-6=39
Dựa vào biểu đồ ven ta có hệ phương trình:
Cộng vế với vế (1),(2),(3) ta có:
a + b + c+2(x+ y + z)=65(5)
Từ (4) và (5) ta có :
a + b + c + 2 (39 – 5 – a – b – c) + 15= 63
⇒ a + b + c = 20
Vậy chỉ có 20 em thích chỉ một trong ba môn trên.
Bài 7: Cho hai tập khác rỗng : A=(m – 1;4], B=(-2;2m + 2), với m ∈ R . Xác định m để:
| a) A ∩ B= ∅ ; | b) A ⊂ B; |
| c) B ⊂ A | D) (A ∩ B) ⊂ (-1;3) |
Với A = (m – 1; 4], B=(-2;2m + 2) là các tập khác tập rỗng, ta có điều kiện:
Với điều kiện (*), ta có :
A ∩ B= ∅ ⇔ m – 1 < 2m + 2⇔ m > -3
So sánh với (*) ta thấy các giá trị m thỏa mãn yêu cầu A ∩ B= ∅ là -2 < m < 5.
b) A ⊂ B⇔
So sánh với (*) ta thấy các giá trị m thỏa mãn yêu cầu A ⊂ B là 1 < m <5.
c) B ⊂ A⇔
So sánh với (*) ta thấy các giá trị m thỏa mãn yêu cầu B ⊂ A là -2 < m ≤ -1.
d) (A ∩ B) ⊂ (-1;3) ⇔
Bài 8:
Quy tròn số 3,258 đến hàng phần trăm là 3,26
Sai số tuyệt đối khi quy tròn đến hàng phần trăm là:
Δ=|3,26-3,258|=0,02
Bài 9:
a) a− = 17658 ± 36;
Vì độ chính xác d = 36 nên ta quy tròn đến hàng trăm.
Số quy tròn là 17700
b) (a)−−−= 15,318 ± 0,046.
Vì độ chính xác d = 0,046 nên ta quy tròn đến hàng phần chục
Số quy tròn là 15,3.
2.Một số bài tập trắc nghiệm
Bài 1: Câu nào sau đây không phải là mệnh đề:
| A.3 + 1 > 10 | B. Hôm nay trời lạnh quá! |
| C. Π là số vô tỷ | D. 2 ∈ Q |
Bài 2: Cho mệnh đề: A:”∀x ∈ R: x2>x. Phủ định của mệnh đề A là:
| A.∀x ∈ R: x2 < x | B.∀x ∈ R: x2 ≠ x |
| C.∃x ∈ R: x2 ≠ x | D.∃x ∈ R: x2 ≤ x |
Bài 3: Chọn mệnh đề đúng:
| A.∃x ∈ R: x2 ≤ x | B.∀x ∈ R: 15x2 – 8x + 1 > 0 |
| C.∃x ∈ R: |x| < 0 | D.∃x ∈ R: (-x)2 > 0 |
Bài 4: Cho tập hợp A={3k|k ∈ N,-2 < k ≤ 3}. Khi đó tập A được viết dưới dạng liệt kê các phần tử là:
| A. {-6; -3; 0; 3; 6; 9} | |
| C. {-3; 0; 3; 6; 9} | D. {-1; 0; 1; 2; 3} |
Bài 5: Hãy chọn mệnh đề sai:
A.√(5 )không phải là số hữu tỷ
B. ∃x ∈ R: 2x > x2
C. Mọi số nguyên tố đều là số lẻ
D. Tồn tại hai số chính phương mà tổng bằng 13
Bài 6: Các phần tử của tập hợp M={x ∈ R|x2 + x + 1 = 0} là:
| A.M=0 | B.M={0} |
| C.M= ∅ | D.M={ ∅ } |
Bài 7: Các phần tử của tập hợp M={x ∈ R|2x2 – 5x + 3 = 0} là:
| A.M=0 | B.M={0} |
| C.M={1;5} | 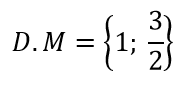 |
Bài 8: Cho:
| A là tập hợp các tứ giác | B là tập hợp các hình bình hành |
| C là tập hợp các hình chữ nhật | D là tập hợp các hình vuông |
Trong các khẳng định sau, khẳng định nào sai?
(I) C ⊂ B ⊂ A
(II) C ⊂ D ⊂ A
(III) D ⊂ B ⊂ A
| A. (I) | B. (II) |
| C. (III) | D. (I) và (III) |
Bài 9: Tập hợp A có 3 phần tử. Vậy tập hợp A có bao nhiêu tập hợp con?
| A. 2 | B. 4 |
| C. 8 | D. 18 |
Bài 10: Tập hợp (-2; 3 ] \ ( 2; 4] là tập hợp:
| A. ∅ | B.{3} |
| C. {-2; 3} | D. (-2; 2) |
Bài 11: Số phần tử nguyên của tập hợp A={k2 + 1|k ∈ R và |k| ≤ 2} là
| A. 1 | B. 2 |
| C. 3 | D. 5 |
Bài 12: Cho hai tập hợp A={k2 |k ∈ N và |k| ≤ 1} và
B={x ∈ R|x3 – 3x2 + 2x = 0}. Tập hợp A\B là
| A.∅ | B.{0;1} |
| C.{2} | D.{0;1;2} |
Bài 13: Cho hai tập hợp:A=(-∞;-3) ∪ [2; +∞) và B=(-5;4). Tính A ∩ B
| A.(-3;2) | B.(-5; -3) ∪ [2;4) |
| C.(-∞;-5) ∪ {2;4} | D.(-5;2) |
Bài 14: Số phần tử của tập hợp A={x ∈ R|(x2 – x)(x4 – 4x2 + 3)= 0} là
| A. 6 | B. 2 |
| C. 3 | D. 5 |
Bài 15: Cho 3 tập hợp: A=[-3;5);B=[-4;1];C=(-4;-3]. Tìm câu sai?
| A.A ∩ B=(-3;1] | B.(A ∪ B) ∪ C=[-4;5] |
| C.CB C=(-3;1] | D.B\A=[-4; -3) |
Bài 16: Cho hai tập hợp: X={1;3;4;5;6}và Y={2;4;6;8}. Tính X ∩ Y
| A.{1;2;3;4} | B.{2; 4;6} |
| C.{4;6} | D.{1;3} |
Bài 17: Cho hai tập hợp: E={x ∈ R|f(x)=0},F={x ∈ R| g(x)=0}, và tập hợp G={x ∈ R|f2 (x) + g2 (x)= 0}. Mệnh đề nào sau đây đúng?
| A.G=E ∩ F | B.G=E ∪ F |
| C.G=E\F | D.G=F\E |
Bài 18: Cho hai tập hợp: E={x ∈ R|f(x)=0},F={x ∈ R| g(x)=0}, và tập hợp 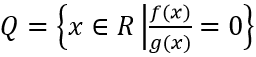
| A.Q=E ∩ F | B.Q=E ∪ F |
| C.Q=E\F | D.Q=F\E |
Bài 19: Mệnh đề nào sau đây tương đương với mệnh đề: A≠∅?
| A.∀x:x ∈ A | B.∃x:x ∈ A |
| C.∃x:x∉A | D.∀x:x∉A |
Bài 20: Cho mệnh đề “∀m ∈ R:phương trình x2-2x-m2=0 có nghiệm “.
Phủ định mệnh đề này là:
A. “∀m ∈ R:phương trình x2 – 2x – m2= 0 vô nghiệm”
B. “∀m ∈ R:phương trình x2 – 2x – m2= 0 có nghiệm kép”
C. “∃m ∈ R:phương trình x2 – 2x – m2= 0 vô nghiệm”
D. “∃m ∈ R:phương trình x2 – 2x – m2= 0 có nghiệm kép”
Đáp án và hướng dẫn giải
| 1B | 2D | 3A | 4C |
| 5C | 6C | 7D | 8B |
| 9C | 10D | 11D | 12A |
| 13B | 14D | 15B | 16C |
| 7A | 18C | 19B | 20C |
Bài 4: A={3k|k ∈ N,-2 < k ≤ 3}
k ∈ N,-2 < k ≤ 3 ⇒ k ∈ {-1;0;1;2;3}
⇒ 3k ∈ {-3;0;3;6;9}
Vậy A={-3;0;3;6;9}.
Bài 9: Tập hợp A có 3 phần tử ⇒ Số tập hợp con là 23 = 8
Bài 12:
A={k2 |k ∈ N và |k| ≤ 1} ⇒ A={0;1}
B={x ∈ R|x3 – 3x2 + 2x = 0} ⇒ B={0;1;2}
⇒ A\B = ∅
Bài 13:
Bài 14: A={x ∈ R|(x2 – x)(x4 – 4x2 + 3)= 0}
(x2 – x)(x4 – 4x2 + 3)= 0 ⇒
⇒
Vậy A có 5 phần tử.
Bài 15: A=[-3;5);B=[-4;1];C=(-4;-3]
Ta có: A ∪ B=[-4;5)
⇒ (A ∪ B) ∪ C=[-4;5)
Chọn đáp án B.
Bài 17: E={x ∈ R|f(x)=0},F={x ∈ R| g(x)=0},
G={x ∈ R|f2 (x) + g2 (x)= 0}
Ta có: f2 (x) + g2 (x)= 0 ⇔
Do đó: G=E∩F.
Bài 18: E={x ∈ R|f(x)=0},F={x ∈ R| g(x)=0},
Ta có: (f(x))/(g(x))=0 ⇔
Do đó: Q=E\F.
Tham kháo:
100 câu trắc nghiệm mệnh đề tập hợp