BÀI TẬP TỔ HỢP XÁC SUẤT KHÓ
- “Bài tập tổ hợp xác suất khó” gồm có 2 phần lớn: Phần A – Tóm tắt lý thuyết cơ bản về tổ hợp xác suất, Phần B – Bài tập tổ hợp xác suất khó.
- Phần A gồm có 2 phần: Tóm tắt lý thuyết về tổ hợp + Tóm tắt lý thuyết về xác suất.
- Phần B gồm có 3 link bài tập: Tổ hợp xác suất thi đại học, 75 câu trắc nghiệm tổ hợp xác suất, 30 câu tổ hợp xác suất.
PHỤ HUYNH VÀ HỌC SINH CÓ THỂ TÌM HIỂU THÊM
Tổ hợp xác suất – Những điều cần biết
Chuyên đề tổ hợp xác suất lớp 11
A. Tóm tắt lý thuyết cơ bản về tổ hợp xác suất:
I. Tổ hợp:
1. Qui tắc đếm:
a. Qui tắc cộng:
Một công việc nào đó có thể được thực hiện theo 1 trong 2 phương án A hoặc B. Nếu phương án A có a cách thực hiện, phương án B có b cách thực hiện (không trùng với bất kỳ cách nào trong phương án A) thì công việc đó có a+b cách thực hiện.
b. Qui tắc nhân:
Một công việc nào đó bao gồm 2 công đoạn A và B. Nếu công đoạn A có a cách thực hiện, ứng với a cách thực hiện đó có b cách thực hiện công đoạn B thì công việc đó có a.b cách thực hiện.
2. Hoán vị:
a. Giai thừa:
n! = 1.2.3….n = (n-1)! . n
![]()
![]()
*Qui ước: 0! = 1
b. Hoán vị (không lặp)
Một tập hợp gồm n phần tử (n≥1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là 1 hoán vị của n phần tử.
Số các hoán vị của n phần tử là: Pn = n!
c. Hoán vị lặp:
Cho k phần tử khác nhau a1, a2,…,ak. Một cách sắp xếp n phần tử trong đó gồm n1 phần tử a1, n2 phần tử a2,…., nk phần tử ak (n1+n2+…+nk = n) theo một thứ tự nào đó được gọi là một hoán vị lặp cấp n và kiểu (n1,n2,…,nk) của k phần tử.
Số hoán vị lặp cấp n và kiểu (n1,n2,…,nk) của k phần tử là:

d. Hoán vị vòng quanh:
Cho tập A gồm n phần tử. Một cách sắp xếp n phần tử thuộc tập A thành 1 dãy kín được gọi là một hoán vị vòng quanh của n phần tử.
Số các hoán vị vòng quanh của n phần tử là Qn = (n-1)!
3. Chỉnh hợp:
a.Chỉnh hợp (không lặp):
– Cho tập hợp A gồm n phần tử. Mỗi cách sắp xếp k phần tử của A (1≤k≤n) theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử của tập A.
– Số chỉnh hợp chập k của n phần tử:
![]()
-Công thức trên cũng đúng trong trường hợp k = 0 hoặc k = n
– Khi k = n thì Ann = Pn = n!
b. Chỉnh hợp lặp:
– Cho tập A gồm n phần tử. Mỗi dãy gồm k phần tử của A, trong đó mỗi phần tử có thể được lặp lại nhiều lần, được sắp xếp theo 1 thứ tự nhất định được gọi là một chỉnh hợp lặp chập k của n phần tử của tập A.
– Số chỉnh hợp lặp chập k của n phần tử : ![]()
4. Tổ hợp:
a. Tổ hợp không lặp:
- Cho tập A gồm n phần tử. Mỗi tập con gồm k (1≤k≤n) phần tử của A được gọi là một tổ hợp chập k của n phần tử.
- Số các tổ hợp chập k của n phần tử:

- Qui ước:
![]()
- Tính chất:
![]()
![]()
![]()
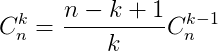
b. Tổ hợp lặp:
Cho tập A = {a1,a2,…,an} và số tự nhiên k bất kỳ. Một tổ hợp lặp chập k của n phần tử là một tổ hợp gồm k phần tử, trong đó mỗi phần tử là một trong n phần tử của A.
Số tổ hợp lặp chập k của n phần tử: ![]()
5. Nhị thức Newton:
a. Công thức khai triển nhị thức Newton:
- ∀n∈N và với mọi cặp số a, b; ta có:

b. Tính chất:
- Số các số hạng của khai triển bằng n+1
- Tổng các số mũ của a và b trong mỗi số hạng bằng n
- Số hạng tổng quát (thứ k+1) có dạng:

- Các hệ số của các cặp số hạng cách đều số hạng đầu và số hạng cuối thì bằng nhau:


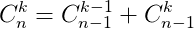
II. Xác suất:
- Xác suất của biến cố:

- 0 ≤ P(A) ≤ 1
- P(Ω) = 1 ; P(∅)= 0
- Qui tắc cộng:
+) Nếu A ∩ B = ∅ thì P(A∪B) = P(A) + P(B)
+) Nếu A, B bất kì thì P(A∪B) = P(A) + P(B) – P(A.B)
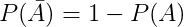
- Qui tắc nhân: Nếu A, B độc lập thì P(A.B)= P(A).P(B)