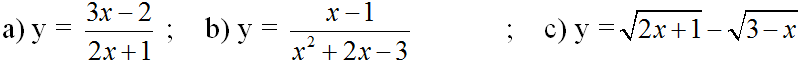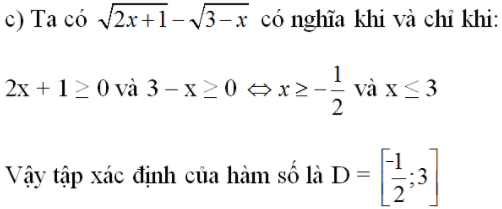Hàm số
Bài 1 (trang 38 SGK Đại số 10): Tìm tập xác định của hàm số:
Lời giải:
⇔ x2 – x + 3x – 3 ≠ 0
⇔ (x – 1)(x + 3) ≠ 0
⇔x ≠ 1 và x ≠ -3
Vậy tập xác định của hàm số là D = R \ {1; -3}
Bài 2 (trang 38 SGK Đại số 10): Cho hàm số
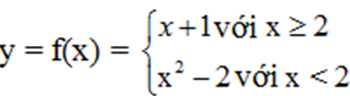
Lời giải:
– Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.
– Ta có : x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.
– Ta có : x = 2 nên f(2) = 2 + 1 = 3.
Bài 3 (trang 39 SGK Đại số 10): Cho hàm số y = 3x2 – 2x + 1. Các điểm sau có thuộc đồ thị của hàm số không ?
a) M(-1 ; 6)
b) N(1 ; 1)
c) P(0 ; 1)
Lời giải:
Lưu ý:
Điểm A(xo, yo) thuộc đồ thị (G) của hàm số y = f(x) có tập xác định D khi và chỉ khi:
Tập xác định của hàm số y = f(x) = 3x2 – 2x + 1 là D = R
a) Ta có: -1 ∈ R, f(-1) = 3(-1)2 – 2(-1) + 1 = 6
Vậy điểm M(-1; 6) thuộc đồ thị hàm số.
b) Ta có: 1 ∈ R, f(1) = 3.12 – 2.1 + 1 = 2 ≠ 1
Vậy N(1; 1) không thuộc đồ thị hàm số.
c) Ta có: 0 ∈ R, f(0) = 3.02 – 2.0 + 1 = 1
Vậy điểm P(0 ; 1) thuộc đồ thị hàm số.
Bài 4 (trang 39 SGK Đại số 10): Xét tính chẵn lẻ của các hàm số sau:
a) y = |x|;
b) y = (x + 2)2;
c) y = x3 + x;
d) y = x2 + x + 1.
Lời giải:
a) Đặt y = f(x) = |x|. Tập xác định D = R.
Do đó mọi x ∈ D thì –x ∈ D.
Mặt khác: f(–x) = |-x| = |x| = f(x) với f(x) = |x|.
Vậy hàm số y là hàm số chẵn.
b) Đặt y = f(x) = (x + 2)2. TXĐ: D = R
Do đó ∀x ∈ D thì –x ∈ D.
Ta có f(-x) = (-x + 2)2 = (x – 2)2 ≠ f(x).
Vậy hàm số y không chẵn, không lẻ.
c) Đặt y = f(x) = x3 + x. TXĐ: D = R.
Do đó ∀x ∈ D thì –x ∈ D.
Ta có f(-x) = (-x)3 + (-x) = -(x3 + x)= -f(x)
Vậy y = f(x) là một hàm số lẻ.
d) Đặt y = f(x) = x2 + x + 1. TXĐ: D = R.
Do đó ∀x ∈ D thì –x ∈ D.
Ta có f(-x) = (-x)2 + (-x) + 1 = x2 + x + 1 ≠ f(x)
Vậy hàm số y không chẵn, không lẻ.