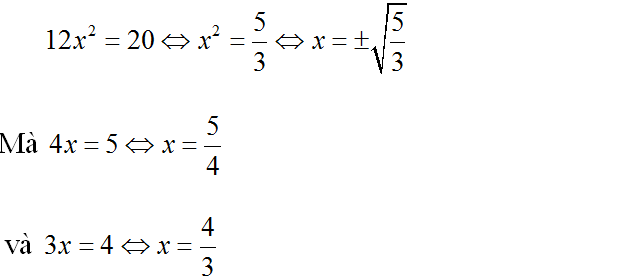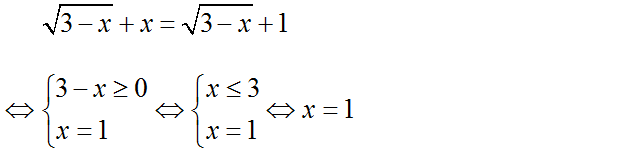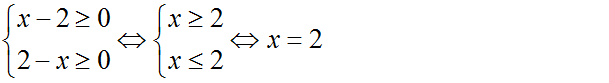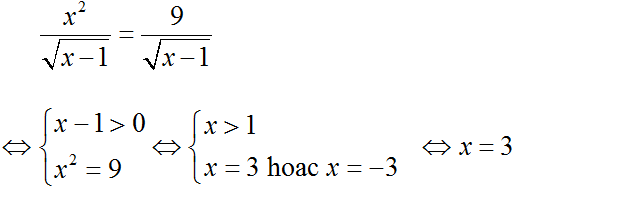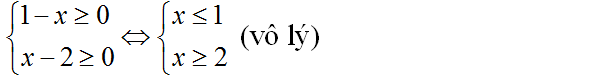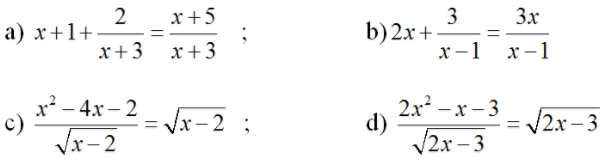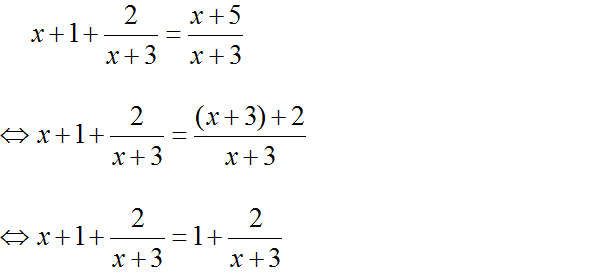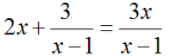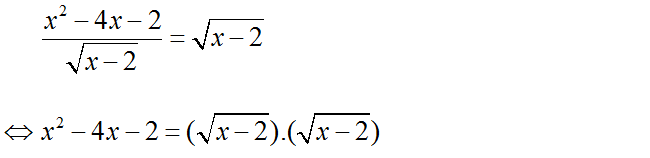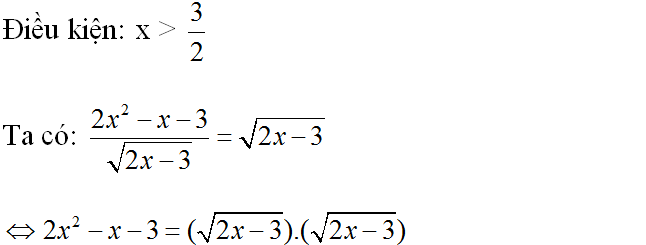Đại cương về phương trình

Bài 1 (trang 57 SGK Đại số 10): Cho hai phương trình:

3x = 2 và 2x = 3

Cộng các vế tương ứng của hai phương trình đã cho. Hỏi:

a) Phương trình nhận được có tương đương với một trong hai phương trình đã cho hay không?

b) Phương trình đã cho có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không?

Lời giải:

a) Cộng các vế tương ứng của hai phương trình ta được:

5x = 5 ⇔ x = 1

Trong khi:

3x = 2 ⇔ x = 2/3

và 2x = 3 ⇔ x = 3/2

Nên phương trình mới không tương đương với một trong hai phương trình đã cho.

b) Phương trình này không phải là phương trình hệ quả của một trong hai phương trình. Bởi vì nghiệm của một trong hai phương trình đã cho không phải là nghiệm của phương trình mới.

Bài 2 (trang 57 SGK Đại số 10): Cho hai phương trình:

            4x = 5 và 3x = 4

Nhân các vế tương ứng của hai phương trình đã cho. Hỏi:

a) Phương trình nhận được có tương đương một trong hai phương trình đã cho hay không?

b) Phương trình đó có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không?

Lời giải:

Nhân các vế tương ứng của hai phương trình đã cho ta được phương trình:

a) Phương trình nhận được không tương đương một trong hai phương trình đã cho vì chúng không có cùng tập nghiệm (không tuân thủ theo phép biến đổi tương đương).

b) Phương trình nhận được không là phương trình hệ quả của một trong hai phương trình đã cho vì nó không chưa tập nghiệm của một trong hai phương trình đã cho.

Bài 3 (trang 57 SGK Đại số 10): Giải các phương trình

Lời giải:

a) Ta có:

Vậy phương trình có nghiệm duy nhất x = 1

b) Điều kiện:

Giá trị x = 2 nghiệm đúng với phương trình nên phương trình có nghiệm duy nhất x = 2.

c) Ta có:

Vậy phương trình có nghiệm duy nhất x = 3

d) Điều kiện:

Vậy phương trình đã cho vô nghiệm.

Bài 4 (trang 57 SGK Đại số 10): Giải các phương trình

Lời giải:

a) Điều kiện: x ≠ 3

Ta có:

⇔ x + 1 = 1

⇔ x = 0 (thỏa mãn điều kiện)

Vậy phương trình có nghiệm x = 0.

b) Điều kiện: x ≠ 1

Ta có:

⇔ 2x(x – 1) + 3 = 3x

⇔ 2x² – 2x + 3 = 3x

⇔ 2x² – 5x + 3 = 0

⇔ (x – 1)(2x – 3) = 0

⇔ x₁ = 1 (loại); x₂ = 3/2 (thỏa mãn)

Vậy phương trình có nghiệm x = 3/2.

(Phương trình có a + b + c = 2 – 5 + 3 = 0 nên phương trình có 1 nghiệm: x₁ = 1)

c) Điều kiện: x > 2

Ta có:

⇔ x² – 4x – 2 = x – 2

⇔ x² – 5x = 0

⇔ x(x – 5) = 0

⇔ x = 0 (loại)

    x = 5 (thỏa mãn điều kiện)

Vậy phương trình có nghiệm x = 5.

d)

⇔ 2x² – x – 3 = 2x – 3

⇔ 2x² – 3x = 0

⇔ x(2x – 3) = 0

⇔ x = 0 (loại)

    x = 3/2 (loại)

Vậy phương trình đã cho vô nghiệm.