BÀI TẬP BẤT PHƯƠNG TRÌNH CƠ BẢN (có đáp án)

• Bài tập về bất phương trình dạng cơ bản gồm có các bài tập về bất phương trình chứa căn thức, bất phương trình chứa trị tuyệt đối, bất phương trình mũ, bất phương trình logarit, bất phương trình bậc 1 và bất phương trình bậc 2. Trong đó, mỗi phần đều có tóm tắt lý thuyết cơ bản cần dùng và bài tập bao gồm tất cả các dạng.
• Ở phần 2 của “Bài tập bất phương trình cơ bản”, phụ huynh và các em học sinh có thể tham khảo bài tập và lý thuyết tóm tắt của bất phương trình mũ và bất phương trình logarit.

PHỤ HUYNH VÀ CÁC EM HỌC SINH CÓ THỂ THAM KHẢO THÊM:

Bất phương trình – Các loại bất phương trình

Bài tập bất phương trình cơ bản (P1)

Bất phương trình hay lạ khó (P1)

I. Bất phương trình mũ:

1.Tóm tắt lý thuyết về bất phương trình mũ:

Thông thường, ta sẽ giải các bất phương trình mũ cơ bản qua phương pháp logarit hóa trên cơ sở sử dụng tính chất đơn điệu của hàm số logarit.

• Nếu b > 0 và a > 1 thì:

– a^x > b => x > log_ab

– a^x ≥ b => x ≥ log_ab

– a^x < b => x < log_ab

– a^x ≤ b => x ≤ log_ab

• Nếu b >0 và 0 < a < 1 thì:

– a^x > b => x < log_ab

– a^x ≥ b => x ≤ log_ab

– a^x < b => x > log_ab

– a^x ≤ b => x ≥ log_ab

• Nếu b ≤ 0 thì các bất phương trình mũ như a^x > b và a^x ≥ b đúng với mọi x thuộc tập R.
• Nếu b ≤ 0 thì các bất phương trình mũ như a^x < b và a^x ≤ b
• Tìm hiểu thêm về lý thuyết cũng như các phương pháp giải bất phương trình mũ ở đây

2. Bài tập bất phương trình mũ cơ bản:

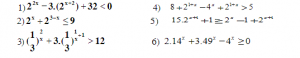
II. Bất phương trình logarit:

1.Tóm tắt lý thuyết về bất phương trình logarit:

Thông thường, ta sẽ giải các bất phương trình logarit đơn giản thường gặp qua phương pháp mũ hóa trên cơ sở sử dụng tính đơn điệu của hàm số mũ.

– Nếu a > 1 thì

log_ax  > b ⇔ x > a^b ;

log_ax ≥  b ⇔ x ≥ a^b

log_ax  < b ⇔ 0 < x < a^b ;

log_ax ≤  b ⇔ 0 < x ≤ a^b

– Nếu 0 < a< 1 thì

log_ax  > b ⇔ 0 < x < a^b ;

log_ax ≥  b ⇔ 0 < x ≤ a^b

log_ax  < b ⇔ x > a^b ;

log_ax ≤  b ⇔ x ≥  a^b

• Tìm hiểu thêm về lý thuyết và các phương pháp giải bất phương trình logarit ở đây.

2.Bài tập cơ bản về bất phương trình logarit:

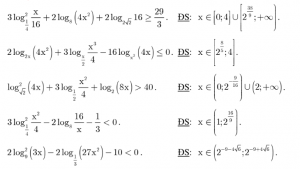
Kết luận: tổng hợp các Bài tập bất phương trình cơ bản (P2) đây là một bài quan trọng