Bài 5. Hệ số góc của đường thẳng y = ax + b (a ≠ 0).

A. Tóm tắt kiến thức:

1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Õ.

Gọi A là giao điểm của đường thẳng y = ax + b với Ox và T là một điểm thuộc đường thẳng, nằm phía trên trục Ox. Khi đó góc TAx được gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Khi a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn.

Khi a < 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng bé thì góc đó càng lớn.

Như vậy, góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào a.

Người ta gọi a là hệ số góc của đường thẳng y = ax + b.

Lưu ý: Khi a > 0, ta có tg 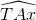 =  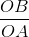=  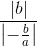=  =  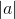= a. Từ đó dùng bảng lượng giác hoặc máy tính bỏ túi suy ra số đo của .

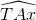Khi a < 0, ta có tg (180⁰ – 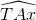) = tg  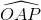=  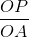=  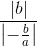=  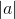= -a.

Từ đó tìm được số đo của góc 180⁰ – 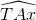 rồi suy ra số đo của góc .

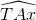B.Bài tập và lời giải chi tiết  

Bài 27. Cho hàm số bậc nhất  $y=ax+3$

a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).

b) Vẽ đồ thị của hàm số.

Giải:

Hàm số đi qua điểm $A(2;6)$

$\Rightarrow 6=2a+3\Rightarrow a=\frac{\mathrm{3/}}{2}$

Câu b:

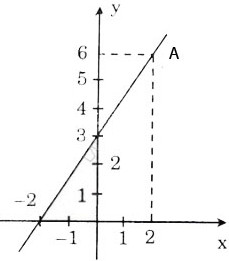
Vẽ đồ thị hàm số:   $y=\frac{\mathrm{3/}}{2}x+3$

Hàm số qua các điểm:

$A(-2;0);B(0;3)$

Đồ thị được vẽ như hình bên.

Bài 28. Cho hàm số  $y=-2x+3.$

a) Vẽ đồ thị của hàm số.

b) Tính góc tạo bởi đường thẳng $y=-2x+3$ và trục Ox (làm tròn đến phút).

Giải:

a) Đồ thị được vẽ như hình bên.

                                         

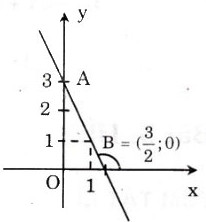
b) Gọi $\alpha$ là góc giữa đường thẳng $y=-2x+3$ và trục Ox.

Ta có: $\widehat{ABO}={\mathrm{180\prime }}^{}-\alpha$

Có: $tg\widehat{ABO}=\frac{O\mathrm{A/}}{OB}=\frac{\mathrm{3/}}{1,5}=2$

Suy ra $\widehat{ABO}\approx {\mathrm{63\prime \; 26″}}^{}$

Vậy $\alpha \approx {\mathrm{116\prime }}^{}{\mathrm{34″}}^{}$

Bài 29. Xác định hàm số bậc nhất $y=ax+b$ trong mỗi trường hợp sau:

a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5.

b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2).

c) Đồ thị của hàm số song song với đường thẳng $y=\sqrt{\mathrm{3X}}$và đi qua điểm $B\left(1;\sqrt{3}+5\right)$

Giải:

a) Hàm số đã cho là y = 2x + b.

Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b.

Suy ra b = -3.

Vậy hàm số đã cho là y = 2x – 3.

b) Hàm số đã cho là y = 3x + b.

Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b.

Suy ra b = -4.

Vậy hàm số đã cho là y = 3x – 4.

c) Vì đồ thị của hàm số đã cho song song với đường thẳng (y = \sqrt 3 x\) nên nó có hệ số góc là $a=\sqrt{3}$ Do đó hàm số đã cho là $y=\sqrt{3}x+b$

Vì đồ thị đi qua điểm $B\left(1;\sqrt{3}+5\right)$nên $\sqrt{3}+5=\sqrt{3}.1+b$.

Suy ra b = 5.

Vậy hàm số đã

Bài 30

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:

$y=\frac{\mathrm{1/}}{2}x+2$                                      $y=-x+2$

b) Gọi giao điểm của hai đường thẳng $y=\frac{\mathrm{1/}}{2}x+2$  và  $y=-x+2$với trục hoành theo thứ tự là $A,B$ và gọi giao điểm của hai đường thẳng đó là $C$. Tính các góc của tam giác $ABC$(làm tròn đến độ).

c) Tính chu vi và diện tích của tam giác $ABC$ (đơn vị đo trên các trục tọa độ là xentimét)

Giải:

a) Đồ thị được vẽ như hình dưới:

                       

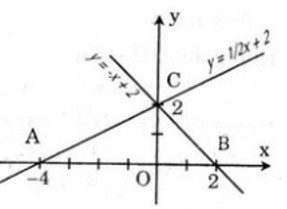
b) Bằng hình vẽ và các phép tính, ta tìm được tọa độ của $3$điểm $A,B,C$đó là:

$A(-4;0);B(2;0);C(0;\mathrm{2)}$

Ta có: $OB=OC$ nên tam giác $COB$ vuông cân tại $O$($O$ là gốc tọa độ) nên:

$\hat{B}={\mathrm{45\prime }}^{}$

Dùng công thức lượng giác đối với tam giác $AOC$ vuông tại $O$, ta có:

$\tan A=\frac{O\mathrm{C/}}{OA}=\frac{\mathrm{1/}}{2}\Rightarrow \hat{A}\approx 26,{\mathrm{56\prime }}^{}$

$\hat{C}={180}^o-\hat{A}-\hat{B}\approx 108,{\mathrm{44\prime }}^{}$

c) Ta có:

$AB=6\left(cm\right)$

$AC=\sqrt{A{O}^2+O{C}^{}}=2\sqrt{5}\left(cm\right)$

$BC=\sqrt{B{O}^2+O{C}^{}}=2\sqrt{2}(c\mathrm{m)}$

Chu vi tam giác là

$P=AB+BC+AC=2(3+\sqrt{5}+\sqrt{2})\left(cm\right)$

Diện tích tam giác:

S=1/2CO.AB=1/2.2.6=6(cm2)

Bài 31

a) Vẽ đồ thị của hàm số :

$y=x+1;y=\frac{\mathrm{1/}}{\sqrt{3}}x+\sqrt{3};y=\sqrt{3}x-\sqrt{3}$

b) Gọi  $\alpha ,\beta ,\gamma$ lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.

Chứng minh rằng $tg\alpha =1,tg\beta =\frac{\mathrm{1/}}{\sqrt{3}};tg\gamma =\sqrt{3}$

Tính số đo các góc α, β, ɣ.

Giải:

a) Đồ thị như hình bên.

                                             

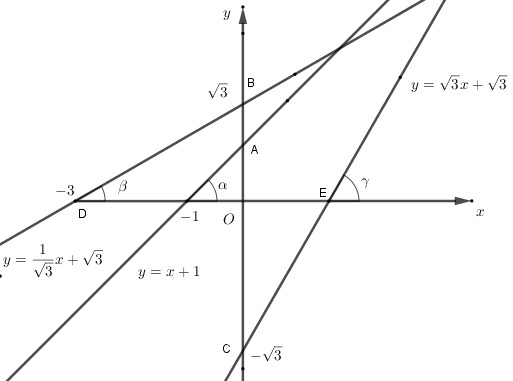
b) Ta có:

$\begin{array}{cc}& tg\alpha =\frac{O\mathrm{E/}}{OA}=1\end{array}$

$\begin{array}{c};\\ & tg\beta =\frac{O\mathrm{P/}}{OB}=\frac{\sqrt{\mathrm{3/}}}{3}=\frac{\mathrm{1/}}{\sqrt{3}};\end{array}$

$\begin{array}{c}\\ & tg\gamma =\frac{O\mathrm{D/}}{OC}=\frac{\sqrt{\mathrm{3/}}}{1}=\sqrt{3}\end{array}$

$\begin{array}{cc}& \Rightarrow \alpha ={45}^{},\beta ={30}^{};\gamma ={60}^{}\end{array}$