Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
A. Lý thuyết về dấu hiệu nhận biết tiếp tuyến của đường tròn
Tóm tắt lý thuyết:
1. Tính chất của tiếp tuyến:
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
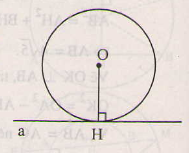
Trong hình trên a là tiếp tuyến.
⇒a⊥OH⇒a⊥OH (H là tiếp điểm).
2. Dấu hiệu nhận biết tiếp tuyến:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn
B. Bài tập
Bài 21 trang 111 sgk Toán 9 – tập 1
Cho tam giác ABC có AB=3, AC=4, BC=5. Vẽ đường tròn (B;BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.
Giải:
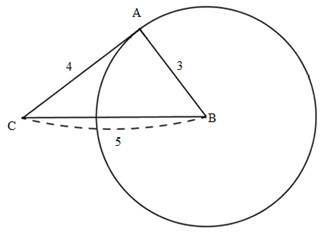
Chứng minh được tam giác ABC vuông tại A (theo định lý Pytago đảo):
BC^2=AC^2+AB^2
⇒AC⊥AB tại A
Vậy AC là tiếp tuyến của đường tròn
Bài 22. Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
Giải:
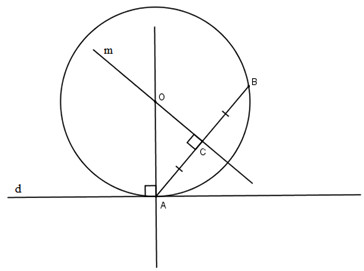
Phân tích:
Giả sử đã dựng được đường tròn thỏa mãn đề bài.
Tâm O thỏa mãn hai điều kện:
– O nằm trên đường trung trực của AB (vì đường tròn đi qua A và B).
– O nằm trên đường thẳng vuông góc với d tại A (vì đường tròn tiếp xúc với đường thẳng d tại A).
Vậy O là giao điểm của hai đường thẳng nói trên.
Cách dựng:
– Dựng đường trung trực m của AB.
– Từ A dựng một đường thẳng vuông góc với d cắt đường thẳng m tại O.
– Dựng đường tròn (O;OA). Đó là đường tròn phải dựng.
Chứng minh:
Vì O nằm trên đường trung trực của AB nên OA=OB, do đó đường tròn (O;OA) đi qua A và B.
Đường thẳng d⊥OA tại A nên đường thẳng d tiếp xúc với đường tròn (O) tại A.
Biện luận: Bài toán luôn có nghiệm hình.
Bài 23. Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm A, B, C. Chiều quay của đường tròn tâm B ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm A và đường tròn tâm C (cùng chiều quay hay ngược chiều quay của kim đồng hồ).
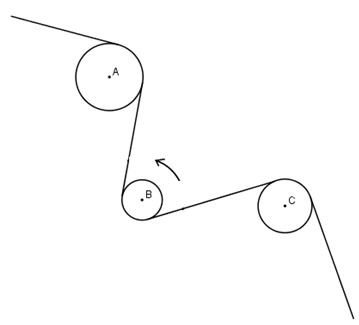
Giải:
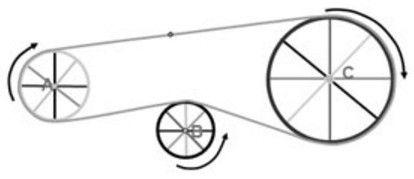
Chiều quay đường tròn tâm A và tâm C cùng chiều kim đồng hồ.
Đường tròn (B) quay ngược chiều với hai đường tròn (A) và (C).
Bài 24. Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.
a) Chứng minh rằng CB là tiếp tuyến của đường tòn.
b) Cho bán kính của đường tròn bằng 15cm, AB=24cm. Tính độ dài OC.
Giải:
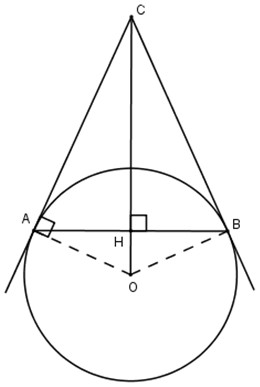
a) Gọi H là giao điểm của OC và AB.
Vì OH⊥AB nên HA=HB, suy ra OC là đường trung trực của AB, do đó CB=CA.
ΔCBO=ΔCAO (c.c.c)
⇒ˆCBO=ˆCAO.
Vì AC là tiếp tuyến của đường trong (O) nên:
AC⊥OA⇒ˆCAO=90∘.
Do đó ˆCBO=90∘.
Vậy CB là tiếp tuyến của đường tròn (O).
b) Xét tam giác HOA vuông tại H, có
OH^2=OA^2−AH^2
=15^2−12^2=81
⇒OH=9(cm)
Xét tam giác BOC vuông tại B, có:
OB^2=OC⋅OH
⇒OC=OB^2/OH=225/9=25(cm).
Nhận xét. Ở câu a) ta đã dùng dấu hiệu nhận biết tiếp tuyến để chứng minh CB là tiếp tuyến của đường tròn (O). Ta cũng có thể dựa vào tính chất đối xứng của đường kính để chứng minh CB là tiếp tuyến. Thực vậy B và A đối xứng qua đường thẳng chứa đường kính CO, mà CA là tiếp tuyến nên CB phải là tiếp tuyến.
Bài 25. Cho đường tròn tâm O có bán kính OA=R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Từ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Hướng dẫn giải:
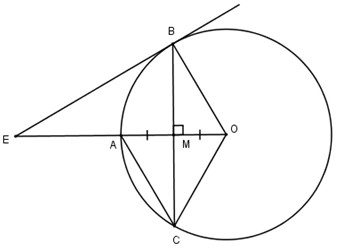
a) Ta có OA⊥BC⇒MB=MC.
Mặt khác:
MA=MO nên tứ giác ABOC là hình bình hành.
Hình bình hành này có hai đường chéo vuông góc nên là hình thoi.
b) Ta có BA=BO (hai cạnh hình thoi) mà BO=OA (bán kính) nên tam giác ABO là tam giác đều.
Suy ra ˆBOA=60∘.
Ta có EB là tiếp tuyến ⇒EB⊥OB
Xét tam giác BOE vuông tại B, có:
BE=BO⋅tg60∘=R.tg60=R√3.