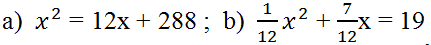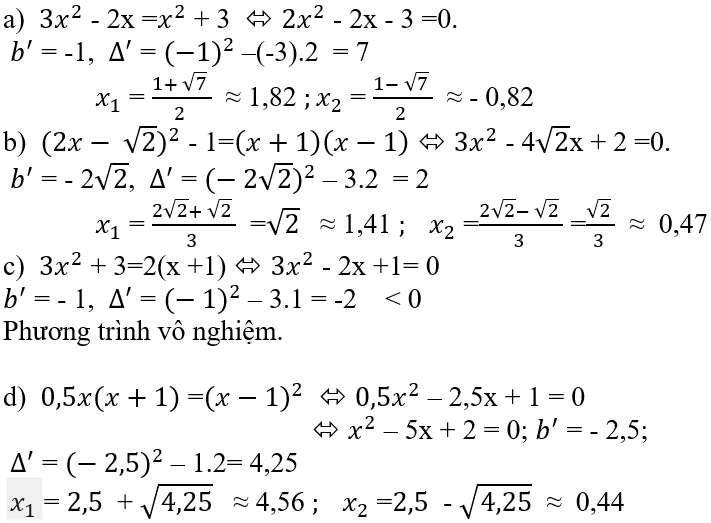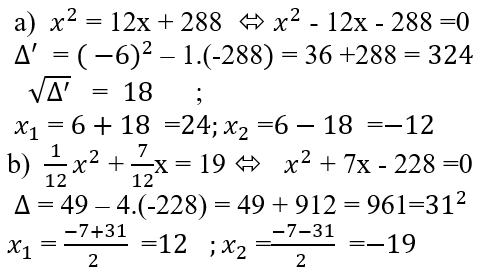Bài 5. Công thức nghiệm thu gọn

1. công thức nghiệm thu gọn

Đối với phương trình $a{\mathrm{x^}}^2+bx+c=0(a\ne 0)$và $b=2b^{}$, ${\Delta }^{\prime }=b{}^{}-ac$

– Nếu ${\Delta }^{\prime }>0$thì phương trình có hai nghiệm phân biệt:

 = $\frac{-b^{\prime }+\sqrt{{△}^{\prime /}}}{a}$; = $\frac{-b^{\prime }-\sqrt{{△}^{\prime /}}}{a}$

– Nếu ${\Delta }^{\prime }=0$ thì phương trình có nghiệm kép

 =$x_2$= $\frac{-b^{\prime /}}{a}$

– Nếu ${\Delta }^{\prime }<0$ thì phương trình vô nghiệm.

2. Chú ý:

– Khi $a>0$ và phương trình $a{\mathrm{x^}}^2+bx+c=0$ vô nghiệm thì biểu thức $a{\mathrm{x^}}^2+bx+c>0$ với mọi giá trị của $x$.

– Nếu phương trình $a{\mathrm{x^}}^2+bx+c=0$ có $a<0$ thì nên đổi dấu hai vế của phương trình để có , khi đó dể giải hơn.

– Đối với phương trình bậc hai khuyết $a{\mathrm{x^}}^2+bx=0$, $a{\mathrm{x^}}^2+c=0$ nên dùng phép giải trực tiếp sẽ nhanh hơn.

B. Bài tập 

Bài 17 (trang 49 SGK Toán 9 tập 2): Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:

Lời giải

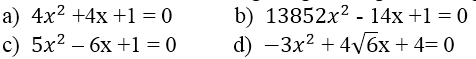
Bài 18 (trang 49 SGK Toán 9 tập 2): Đưa các phương trình sau về dạng ax² + 2b’x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):

Lời giải

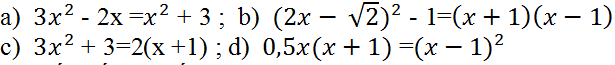
Bài 19 (trang 49 SGK Toán 9 tập 2): Đố. Đố em biết vì sao khi a > 0 và phương trình ax² + bx + c = 0 vô nghiệm thì ax² + bx + c > 0 với mọi giá trị của x?

Lời giải

Bài 20 (trang 49 SGK Toán 9 tập 2): Giải các phương trình:

Lời giải

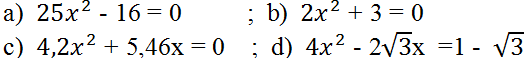
Bài 21 (trang 49 SGK Toán 9 tập 2): Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):

Lời giải