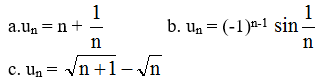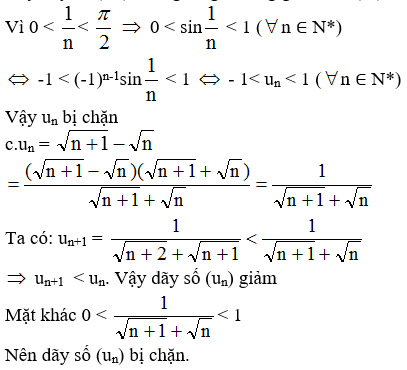a. 13ⁿ – 1 chia hết cho 6

b. 3n³ + 15 chia hết cho 9

Lời giải  Bài 5 (trang 107 SGK Đại số 11)

a. Xét u_n = 13ⁿ – 1

ta có: với n = 1 thì u1 = 13 – 1 = 12 chia hết 6

giả sử: u_k = 13^k – 1 chia hết cho 6

Ta có: u_k+1 = 13^k+1 – 1 = 13^k+1 + 13^k – 13^k – 1

= 13^k(13 – 1) + 13^k – 1

= 12.13^k + u^k

=> u^k+1 là tổng hai số hạng, mỗi số hạng chia hết cho 6.

Vậy u^k+1 chia hết số 6

Như vậy, mỗi số hạng của dãy số (uⁿ) đều chia hết cho 6 ∀n ∈ N*

Đặt u_n = 3n³ + 15n

+ Với n = 1 => u₁ = 18 chia hết 9

+ giả sử với n = k ≥ 1 ta có:

u_k = (3k² + 15k) chia hết 9 (giả thiết quy nạp)

+ Ta chứng minh: u_k+1 chia hết 9

Thật vậy, ta có:

u_k+1 = 3(k + 1)³ + 15(k + 1 ) = 3(k³ + 3k² + 3k + 1) + 15k + 15

= (3k³ + 15k) + 9k² + 9k + 18 = (3k³ + 15) + 9(k² + k + 2)

= u_k + 9(k² + k + 2)

Theo giả thiết u_k chia hết 9, hơn nữa 9(k² + k + 2) chia hết 9 k ≥ 1

Do đó u_k+1 cũng chia hết cho 9.

Vậy u_n = 3n³ + 15n chia hết cho 9 ∀n ∈ ∈ N*

Bài 6 (trang 107 SGK Đại số 11): Cho dãy số (u_n) biết u₁ = 2, u_{n+ 1} = 2u_n – 1 (với n ≥ 1)

a.Viết năm số hạng đầu của dãy.

b.Chứng minh u_n = 2^n-1 + 1 bằng phương pháp quy nạp.

Lời giải Bài 6 (trang 107 SGK Đại số 11)

a. 5 số hạng đầu dãy là:

u₁ = 2; u₂ = 2u₁ – 1 = 3; u₃ = 2u₂ – 1 = 5;

u₄ = 2u₃ – 1 = 9 u₅ = 2u₄ – 1 = 17

b. Chứng minh: u_n = 2^n-1 + 1 bằng phương pháp quy nạp:

Với n = 1 => u₁ = 2^1-1 + 1 = 2 (đúng).

Giả sử (u_n) đúng với n = k ≥ 1

Tức là u_k = 2^k-1 + 1 (1)

Ta phải chứng minh phương trình đã cho đúng với n = k + 1 nghĩa là:

u_k+1 = 2^k+1-1 + 1 = 2^k + 1

Theo giả thiết: u_k+1 =2u_k-1

(1) u_k+1 = 2(2^k-1 + 1) – 1 = 2.2^k.2^-1 + 2 – 1 = 2_k + 1

Biểu thức đã cho đúng với n = k + 1, vậy nó đúng với n ∈ N*

Bài 7 (trang 107 SGK Đại số 11): Xét tính tăng, giảm và bị chặn của các dãy số (u_n), biết:

Lời giải Bài 7 (trang 107 SGK Đại số 11):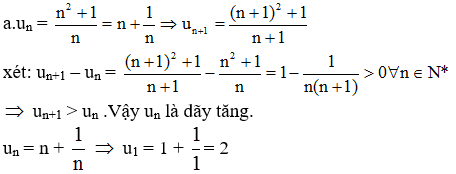

vì là dãy tăng nên u₁ = 2 < u₂ < u₃ < …< u_n ∀n ∈ N*

=> u_n > 2 => (u_n) bị chặn dưới.

Vì u_n = n + 1 > n ∀n ∈ N*

=> (u_n) không bị chặn trên. Vậy u_n không bị chặn.

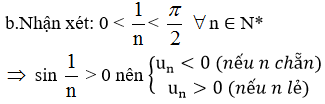
=> u₁ > 0; u₂ > 0; u₃ > 0; u₄ > 0

Và u₁ > u₂; u₂ > u₃; u₃ > u₄; …

Vậy dãy số (u_n ) không tăng, không giảm => (u_n) không đơn điệu.