A. Lý thuyết
1. Đồ thị hàm số y = ax^2 (a ≠ 0)
Đồ thị của hàm số y = ax^2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
– Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
– Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất cảu đồ thị.
2. Cách vẽ đồ thị y = ax^2 (a ≠ 0)
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
B. Bài tập
Bài 4 (trang 36 SGK Toán 9 tập 2): Cho hai hàm số:
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Lời giải
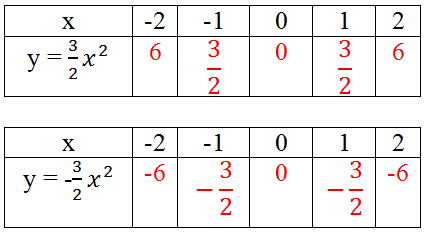
Điền vào ô trống:
Vẽ đồ thị:
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Bài 5 (trang 37 SGK Toán 9 tập 2): Cho ba hàm số:
Lời giải
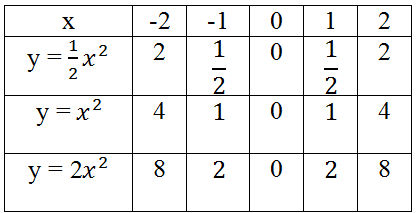
a) Bảng giá trị tương ứng của x và y:
Vẽ đồ thị:
Kiểm tra tính đối xứng: A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 do đó các hàm số có giá trị nhỏ nhất khi x = 0.
Bài 6 (trang 38 SGK Toán 9 tập 2): Cho hàm số y = f(x) = x2.
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √3 ; √7.
Lời giải
a) Lập bảng giá trị tương ứng của x, y và vẽ đồ thị:
Bài 7 (trang 38 SGK Toán 9 tập 2): Trên mặt phẳng tọa độ (h.10), có một điểm M thuộc đồ thị của hàm số y = ax2.
a) Tìm hệ số a.
b) Điểm A(4; 4) có thuộc đồ thị không?
c) Hãy tìm thêm hai điểm nữa(không kể điểm O) để vẽ đồ thị.
Lời giải
c) Nhờ tính đối xứng của đồ thị, chẳng hạn ta lấy thêm hai điểm M'(-2; 1) và A'(-4; 4).
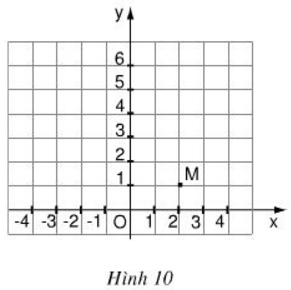
Vẽ đồ thị:
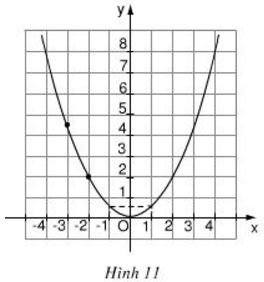
Bài 8 (trang 38 SGK Toán 9 tập 2): Biết rằng đường cong trong hình 11 là một parapol y = ax2.
a) Tìm hệ số a.
b) Tìm tung đệ của điểm thuộc parapol có hoành độ x = -3.
c) Tìm các điểm thuộc parapol có tung độ y = 8.
Lời giải
