Bài 2. Hàm số bậc nhất.

A. Tóm tắt kiến thức:

1. Định nghĩa:

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là những số cho trước và a  ≠ 0.

2. Tính chất:

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:

a) Đồng biến trên R khi a > 0

b) Nghịch biến trên R khi a < 0.

B, Bài tập và lời giải 

Bài 8 trang 48 sgk Toán 9 tập1

Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? Hãy xác định các hệ số a, b của chúng và xét xem hàm số bậc nhất nào đồng biến, nghich biến.

a) y = 1 – 5x;                                         b) y = -0,5x;

c) $y=\sqrt{2}\left(x+1\right)+\sqrt{3}$                    d) y = 2x² + 3.

Giải:

a) y = 1 – 5x là một hàm số bậc nhất với a = -5, b = 1. Đó là một hàm số nghịch biến vì -5 < 0.

b) y = -0,5x là một hàm bậc nhất với a ≈  -0,5, b = 0. Đó là một hàm số nghịch biến vì -0,5 < 0.

c) $y=\sqrt{2}\left(x+1\right)+\sqrt{3}$ là một hàm số bậc nhất với $a=\sqrt{2},b=\sqrt{3}-\sqrt{2}$. Đó là một hàm số đồng biến vì $\sqrt{2}>0$.

d) y = 2x² + 3 không phải là một hàm số bậc nhất vì nó không có dạng y = ax + b, với a ≠ 0.

Bài 9. Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số:

a) Đồng biến;

b) Nghịch biến.

Giải:

a) Hàm số: $y=(m-2)x+3$ đồng biến trên R:

$\iff m-2>0\iff m>2$

b)  Hàm số: $y=(m-2)x+3$ nghịch biến trên R:

$\iff m-2<0\iff m<2$

Bài 10 trang 48 sgk Toán 9 tập 1

Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.

Giải:

Khi bớt mỗi kích thước x (cm) thì được một hình chữ nhật có các kích thước là 20 – x (cm) và 30 – x (cm).

Khi đó chu vi của hình chữ nhật là $y=2\left(20-x+30-x\right)$ hay $y=100-4x$

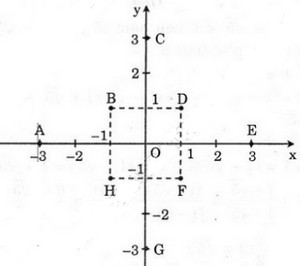
Bài 11. Hãy biểu biễn các điểm sau trên mặt phẳng tọa độ:

A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), E(3; 0), F(1; -1), G(0; -3), H(-1; -1).

Giải:

Xem hình sau:

Bài 12 trang 48 sgk Toán 9 tập 1

Cho hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5.

Giải:

Theo đề bài ta có:

Hàm số: $y=ax+3$ đi qua điểm $A(1;2,5)$

$\iff 2,5=1.a+3\iff a=\frac{-1}{2}$

Và hàm số đó là $y=-\frac{1}{2}x+3$