Bài 2. Đường kính và dây của đường tròn
A. Lý thuyết về đường kính và dây của đường tròn
Tóm tắt kiến thức:
1. So sánh độ dài của đường kính và dây.
Trong các dây của một đường tròn, dây lớn nhất là đường kính.
2. Quan hệ vuông góc giữa đường kính và dây.
– Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
– Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
B. Bài tập
Bài 10. Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE<BC
Giải
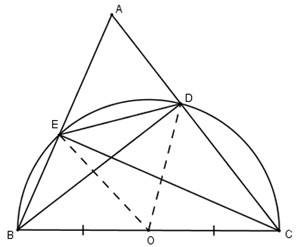
a) Gọi O là trung điểm của BC.
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
EO=1/2BC;DO=1/2BC./
Suy ra OE=OD=OB=OC(=1/2BC)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường (O;BC/2), BC là đường kính, DE là một dây cung không đi qua tâm, do đó DE<BC
Bài 11. Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH=DK
Gợi ý:
Kẻ OM vuông góc với CD.
Giải
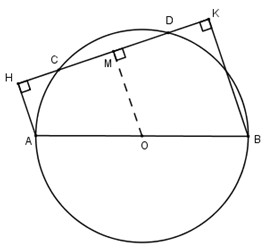
Vẽ OM⊥CD
Xét tam giác OCD có:
{OM⊥CD
OC=OD=AB/2
Tam giác OCD cân tại O có OM là đường cao nên cũng đồng thời là đường trung tuyến.
⇒MC=MD (1)
Xét hình thang AHKB, ta có:
OM//AH//BK (cùng vuông góc với CD)
AO=BO=AB/2
Vậy MO là đường trung bình của hình thang AHKB
⇒MH=MK (2)
Từ (1) và (2) ⇒CH=DK
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm C và D cho nhau