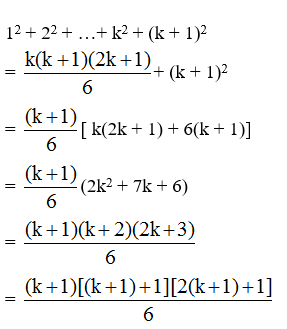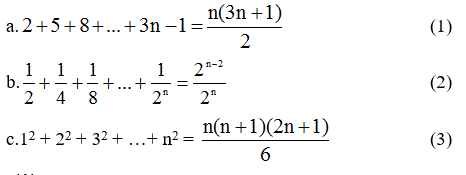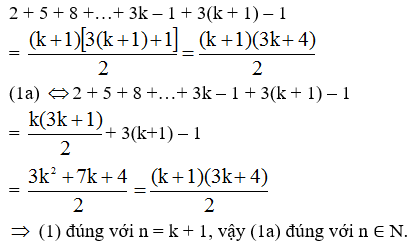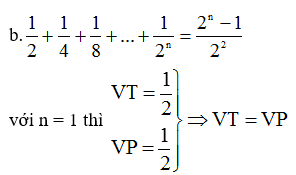Bài 1 (trang 82 SGK Đại số 11): Chứng minh rằng với n ∈ N*, ta có các đẳng thức:
Bài 1 (trang 82 SGK Đại số 11): Chứng minh rằng với n ∈ N*, ta có các đẳng thức:
Lời giải:
a.Với n = 1, ta có:
VT = 3 – 1 = 2
VP = (3 + 1)/2
Vậy VT = VP (1) đúng với n = 1
Giả thiết (1) đúng với n = k ≥ 1 nghĩa là:
2 + 5 + 8 + …+3k – 1 = k(3k+1)/2 (1a)
Ta chứng minh (1a) đúng với n = k + 1 nghĩa là chứng minh:
Vậy (2) đúng với n = 1
Giả sử đẳng thức đúng với n = k, tức là:
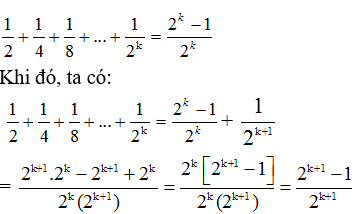
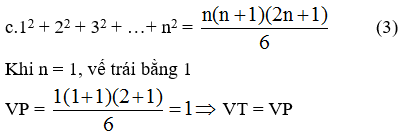
*giả sử đẳng thức (3) đúng với n = k nghĩa là:
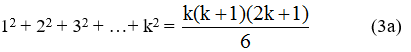
+ Ta cộng 2 vế của (3) cho (k + 1)2