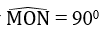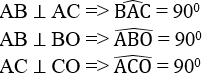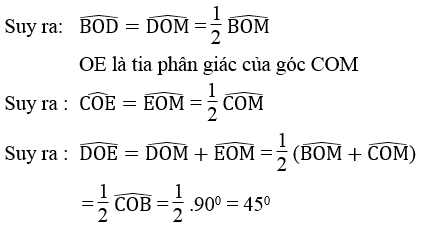Bài 6: Tính chất của hai tiếp tuyến cắt nhau
Bài 48 trang 164 Sách bài tập Toán 9 Tập 1:
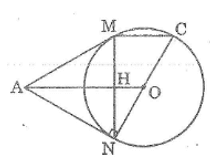
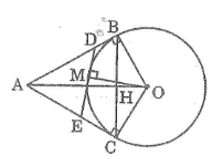
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm)
a. Chứng minh rằng OA ⊥ MN
b. Vẽ đường kính NOC. Chứng minh rằng MC // AO
c. Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm
Lời giải:
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: NM ⊥ MC
Mà OA ⊥ MN (chứng minh trên)
Suy ra: OA // MC
c. Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Bài 49 trang 164 Sách bài tập Toán 9 Tập 1:
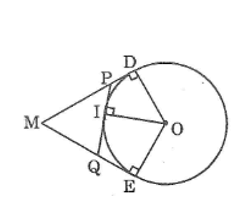
Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ
Lời giải:
Ta có: MD = ME (tính chất hai tiếp tuyến cắt nhau)
PD = PI (tính chất hai tiếp tuyến cắt nhau)
QI = QE (tính chất hai tiếp tuyến cắt nhau)
Chu vi tam giác APQ bằng:
MP + PQ + QM
= MP + PI + IQ + QM
= MP + PD + QM + QE
= MD + ME
= 2.MD
= 2.4 = 8 (cm)
Bài 50 trang 164 Sách bài tập Toán 9 Tập 1:
Cho góc xOy khác góc bẹt, điểm A nằm trên tia Ox. Dựng đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy
Lời giải:
* Phân tích
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
– Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
– Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
– Dựng tia phân giác của góc xOy
– Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
– Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn 180o nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.
Bài 51 trang 164 Sách bài tập Toán 9 Tập 1:
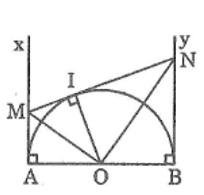
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.
a. Tính số đo góc MON
b. Chứng minh rằng MN = AM + BN
c. Chứng minh rằng AM.BN = R2 (R là bán kính của nửa đường tròn)
Lời giải:
a. Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: 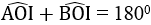
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy
b. Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN
c. Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
OI2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = OI2 = R2
Bài 52 trang 165 Sách bài tập Toán 9 Tập 1:
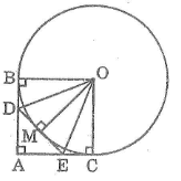
Cho đường tròn (I) nội tiếp tam giác ABC. Các tiếp điểm trên AC, AB theo thứ tự là D, E. Cho BC = a, AC = b, AB = c. Tính độ dài các đoạn tiếp tuyến AD, AE theo a, b, c.
Lời giải:
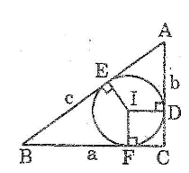
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
AE = AD
BE = BF
CD = CF
Mà: AE = AB – BE
AD = AC – CD
Nên: AE + AD = (AB – BE) + (AC – CD) = AB + AC – (BE + CD)
= AB + AC – (BF + CF) = AB + AC – BC
Suy ra: AE + AD = c + b – a
Hay: AE = AD = (c + b – a)/2
Bài 53 trang 165 Sách bài tập Toán 9 Tập 1:
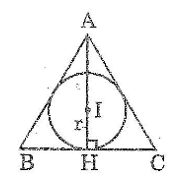
Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I, r)
Lời giải:
Gọi H là tiếp điểm của đường tròn (I) với BC.
Ta có: IH ⊥ BC (tính chất tiếp tuyến)
Vì I là tâm đường tròn nội tiếp tam giác ABC nên AI là tia phân giác của góc BAC
Tam giác ABC đều nên AI cũng là đường cao của tam giác ABC. Khi đó A, I, H thẳng hàng
Ta có: HB = HC (tính chất tam giác đều)
Tam giác ABC đều nên I cũng là trọng tâm của tam giác ABC
Suy ra: AH = 3.HI = 3.r
Bài 54 trang 165 Sách bài tập Toán 9 Tập 1:
Cho đường tròn (O; 3cm) và điểm A có OA = 5cm. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC)
a. Tính độ dài OH
b. Qua điểm M bất kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE
Lời giải:
a. Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau). Suy ra ∆ABC cân tại A.
AO là tia phân giác của góc BAC (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác ABC (tính chất tam giác cân)
Ta có: AO vuông góc với BC tại H
Lại có: AB ⊥ OB (tính chất tiếp tuyến)
Tam giác ABO vuông tại B có BH ⊥ AO
Theo hệ thức lượng trong tam giác vuông, ta có:
OB2 = OH.OA ⇒ OH = OB2/OA = 32/5 = 1,8 (cm)
b. Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
AO2 = AB2 + BO2
Suy ra: AB2 = AO2 – BO2 = 52 – 32 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)
Bài 55 trang 165 Sách bài tập Toán 9 Tập 1:
Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn vuông góc với nhau tại A (B và C là các tiếp điểm)
a. Tứ giác ABOC là hình gì? Vì sao?
b. Gọi M là điểm bất kì thuộc cung nhỏ BC. Qua M kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE.
c. Tính số đo góc DOE
Lời giải:
a. Ta có :
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật
Mặt khác : AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác ABOC là hình vuông
b. Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)
c. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OD là tia phân giác của góc BOM
Bài 56 trang 165 Sách bài tập Toán 9 Tập 1:
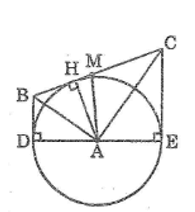
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A;AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
Chứng minh rằng:
a. Ba điểm D, A, E thẳng hàng
b. DE tiếp xúc với đường tròn các đường kính BC
Lời giải:
a. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AB là tia phân giác của góc HAD
Vậy ba điểm D, A, E thẳng hàng.
b. Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có:
AD ⊥ DB; AE ⊥ CE
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: MA // BD ⇒ MA ⊥ DE
Trong tam giác vuông ABC ta có : MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC.